Light is falling on the surfaces S1,S2andS3 as shown below:
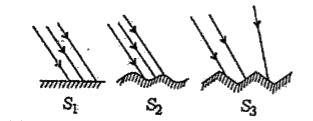
The surfaces on which the angle of incidence is equal to the angle of reflection are
S1andS2
S2andS3
S1andS3
All the three surfaces
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Knowledge Check
Light is falling on the surfaces S1,S2andS3 as shown below.

The surfaces on which the angle of incidence is equal to the angle of reflection areAS1andS3BAll the three surfacesCS1andS2DS2andS3S1 and S2 are two equipotential surfaces on which the potentials are not equal
AS1 and S2 cannot intersect.BS1 and S2 cannot both be plane surfaces.CIn the region between S1 and S2 the field is maximum where they are closest to each other.DA line of force from S1 and S2 must be perpendicular to both.A ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.ADACBBCDABCBACDDDBAC
A light ray strikes a reflective plane surface at an angle of 30∘ with the plane surface.
(i) Find the angle of incidence. (ii) Find the angle of reflection. (iii) Find the angle of between the incident and the reflected ray. (iv) Find the angle between the reflected ray and the plane surface.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionAn unpolarized light beam is incident on a surface at an angle of incidence equal to Brewster's angle. Then,
View SolutionAn upolarized light beam is incident on a surface at an angle of incidence equal to Brewster's angle. Then,
View SolutionA light ray is incident on a smooth reflecting surface making an angle of incidence 2i. If the angle of incidence is doubled, then the deviation of the light ray is equal to ______ .
View Solution

