ABCD is a square E,F,G,H are the mid-point of the four sides.Then the figure EFGH is
square
rectangle
trapezium
parallelogram
The correct Answer is:C
Similar Questions
In the figure given below, ABCD is a square of side 14 cm with E,F,G and H as the mid points of sides. The area of EFGH is :
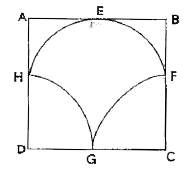 View Solution
View SolutionABCD is a square of area 100cm2. E,F,G,H are the mid points of its sides. K,L,M,N.are the mid points of the sides of EFGH. Find the area of KLMN.
View SolutionABCD is a square . W is the mid point of AB side of square is 16 cm. Find the radius of circle in figure
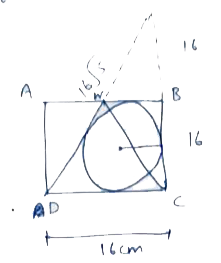 View Solution
View SolutionIn the given figure, ABCD is a rectangle; EandF are the mid-points of the sides BCandCD respectively. What is the ratio of the area of ΔAEF and that of ΔECF?
View SolutionThe given figure shows a quadrilateral ABCD in which E, F, G and H are the midpoints of consecutive sides of ABCD. Again P, Q, R and S are the mid-points of the consecutive sides of quadrilateral EFGH. If EFGH is a rectangle, show that : PQRS is a rhombus.
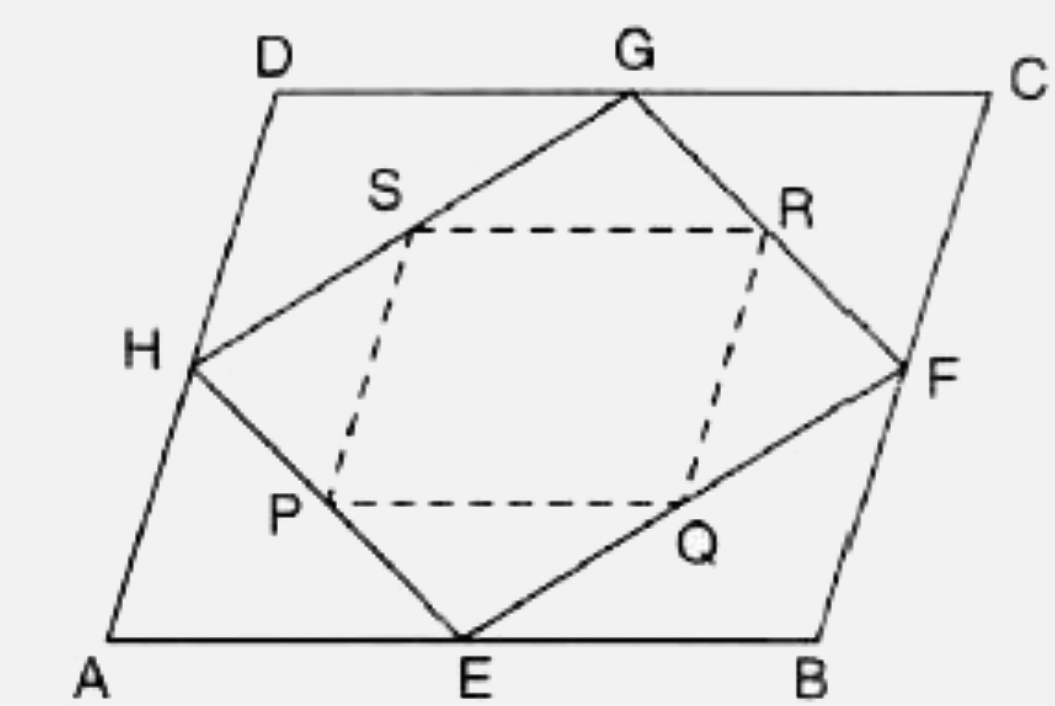 View Solution
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
View SolutionIn the figure given below, ABCD is a square of side 14 cm with E, F, G and H as the mid points of sides AB, BC, CD and DA respectively. The area of the shaded portion is
 View Solution
View SolutionE,F,G,H are respectively, the mid-points of the sides of parallelogram ABCD . Show that the area of EFGH is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join H and F
View SolutionABCD is a parallelogram. E is the mid-point of AB and F is the mid-point of CD. GH is any line that intersects AD, EF and BC at G, P and H respectively. Prove that : GP=PH
 View Solution
View Solution

