A point object is placed on the axis of the concave mirror at a distance of 60 cm from the focal point of the mirror. Its image is formed at the point of object then focal length of the mirror is
15 cm
30 cm
60 cm
120 cm
The correct Answer is:C
To solve the problem, we need to find the focal length of the concave mirror given that a point object is placed at a distance of 60 cm from the focal point and that its image is formed at the point of the object.
1. Understand the Given Information:
- The object is placed at a distance of 60 cm from the focal point of the concave mirror.
- Let the focal length of the mirror be f.
- The distance of the object from the mirror u can be expressed as:
u=f+60cm
- The image is formed at the same point as the object, which means the image distance v is equal to u:
v=−u
(The negative sign indicates that the image is formed on the same side as the object for a concave mirror.)
2. Use the Mirror Formula:
- The mirror formula relates the object distance u, the image distance v, and the focal length f:
1f=1u+1v
3. Substituting Values:
- Since v=−u, we can substitute v in the mirror formula:
1f=1u+1−u=1u−1u=0
- This indicates that the object is at the center of curvature, which is twice the focal length.
4. Finding the Focal Length:
- Since u=f+60, and we know that at the center of curvature u=2f:
2f=f+60
- Rearranging gives:
2f−f=60⟹f=60cm
Final Answer:
The focal length of the concave mirror is 60cm.
- The object is placed at a distance of 60 cm from the focal point of the concave mirror.
- Let the focal length of the mirror be f.
- The distance of the object from the mirror u can be expressed as:
u=f+60cm
- The image is formed at the same point as the object, which means the image distance v is equal to u:
v=−u
(The negative sign indicates that the image is formed on the same side as the object for a concave mirror.)
- The mirror formula relates the object distance u, the image distance v, and the focal length f:
1f=1u+1v
- Since v=−u, we can substitute v in the mirror formula:
1f=1u+1−u=1u−1u=0
- This indicates that the object is at the center of curvature, which is twice the focal length.
- Since u=f+60, and we know that at the center of curvature u=2f:
2f=f+60
- Rearranging gives:
2f−f=60⟹f=60cm
The focal length of the concave mirror is 60cm.
Similar Questions
An object is placed in front of a concave mirror at a distance of 7.5 cm from it. If the real image is formed at a distance of 30 cm from the mirror, find the focal length of the mirror. What would be the focal length if the image is virtual.
View SolutionAn object is placed at a distance of 30 cm from a concave mirror and its real image is formed at a distance of 30 cm from the mirror. The focal length of the mirror is
View Solution
Knowledge Check
An object is present on the principal axis of a concave mirror at a distance 30cmfrom it.Focal length of mirror is20cm
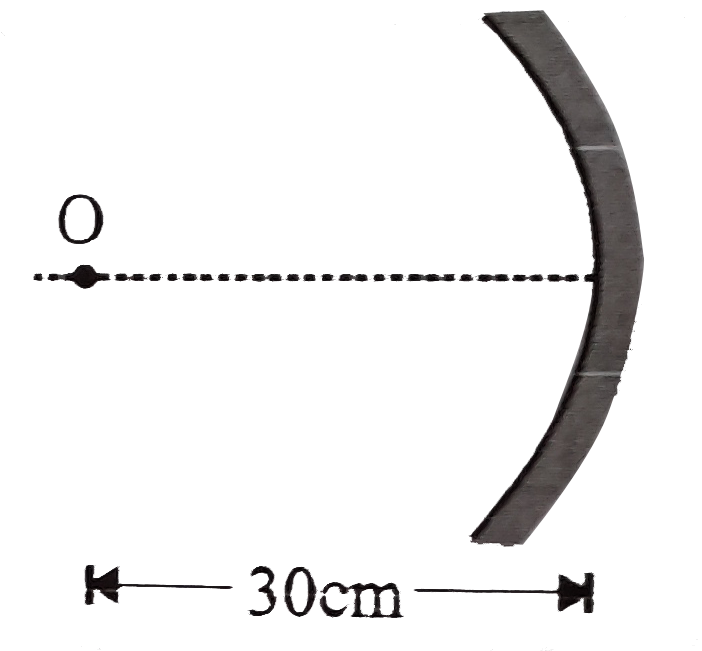
Image formed by mirror isAAt a distance 60cmin front of mirror.BAt a distance 60cmbehind of mirror.CAt a distance 12cmin front of mirror.DAt a distance 12cmbehind of mirror.An object is placed on the principal axis of a concave mirror at a distance of 1.5 f(f is the focal length). The image will be at,
A1.5fB−1.5fC3fD−3fAn object is present on the principal axis of a concave mirror at a distance 30cm from it. Focal length of mirror is 20cm.
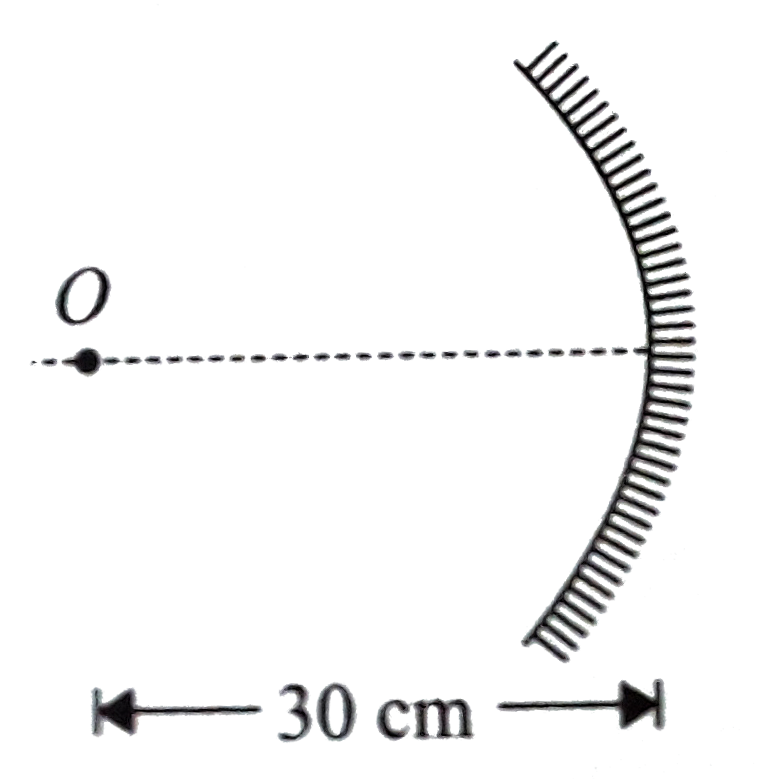
Q. Image formed by mirror isAAt a distance of 60cm in front of mirrorBAt a distance 60cm behind the mirrorCAt a distance 12 cm in front of mirrorDAt a distance 12cm behind the mirror
An object is placed at a distance of 15 cm from a concave mirror and its real image is formed at 30 cm in front of that mirror. The focal length of the mirror is
View SolutionAn object is placed in front of a mirror at a distance of 60cm. If its two times diminished image is formed on the screen, the focal length of the mirror is
View SolutionAn object is placed in front of a convex mirror at a distance equal to the focal length of the mirror. If its focal length is 20 cm, the distance of the image from the mirror is ______ cm
View SolutionAn object is placed at a distance of 25 cm from a spherical mirror, its image is formed behing the mirror at a distance of 5 cm. The focal length and type mirror is
View SolutionAn object is placed at 20 cm from a convex mirror of focal length 20 cm. The distance of the image from the pole of the mirror is
View Solution
