In the figure, if B1,B2,B3, and A1,A2,A3,….. have been marked at equal distances. In what ratio C divides AB?
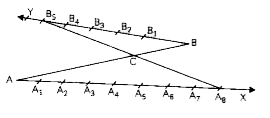
The correct Answer is:8:5
Step by step video & image solution for In the figure, if B_(1), B_(2), B_(3), and A_(1), A_(2), A_(3), ….. have been marked at equal distances. In what ratio C divides AB? by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 01BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART - A (SECTION - II)
14 Videos
- SAMPLE PAPER 01BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 01EXERCISE - PART - B SECTION - III
8 Videos
- SAMPLE PAPER -6 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER -6 EXERCISE - Part - B (Section - V)
6 Videos
- SAMPLE PAPER 02BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 02EXERCISE - SECTION - D
9 Videos
Similar Questions
In the figure, if B1, B2, B3,…... and A1,A2, A3,….. have been marked at equal distances. In what ratio C divides AB?
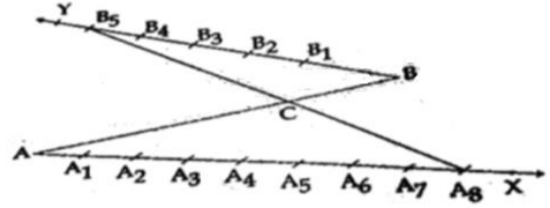
View SolutionIf the arithmetic mean of a1,a2,a3,........an is a and b1,b2,b3,........bn have the arithmetic mean b and ai+bi=1 for i=1,2,3,…….n, prove that n∑i=1(ai−a)2+n∑i=1aibi=nab.
View Solution
Knowledge Check
To divide a line segment AB in the ratio 5:6, draw a ray AX such that ∠BAX is an acute angle, the draw a ray BY parallel to AX and the points A1,A2,A3,….. and B1,B2,B3,….. are located to equal distances on ray AX and BY, respectively. Then, the points joined are
AA5 and B6BA6 and B5CA4 and B5DA5 and B4A1,A2,A3,……,An and B1,B2,B3,….,Bn are non-singular square matrices of order n such that A1B1=In,A2B2=In,A3B3=In,……AnBn=In then(A1A2A3…..An)−1 = ______.
AB1B2B3…BnBB−11B−12B−13…B−1nCBnBn−1Bn−2….B1DBn−1Bn−1−1Bn−2−1...B−11Let a1,a2,a3....andb1,b2,b3... be arithmetic progression such that a1=25,b1=75anda100+b100=100. Then
Athe difference between successive terms in progression 'a' is opposite of the difference in progression 'b'Ban+bn=100 for any nC(a1+b1),(a2+b2),(a3+b3),..... are in A.P.D100∑r=1(ar+br)=10000
Let A and B be two sets such that n(A)=5 and n(B)=2. If (a1,2),(a2,3),(a3,2),(a4,3),(a5,2) are in A×B and a1,a2,a3,a4 and a5 are distinct, find A and B.
View Solutionif Δ=∣∣ ∣∣a1b1c1a2b2c2a3b3c3∣∣ ∣∣
View Solutionif a,A1,A2,A3.......,A2n,b are in A.P. then 2n∑i=1Ai=(a+b)
View SolutionIf vectors ¯a≡(a1,a2,a3) and ¯b≡(b1,b2,b3) are collinear/coincident/parallel, then, in general,
View SolutionIf a and b are distinct positive real numbers such that a,a1,a2,a3,a4,a5,b are in A.P. , a,b1,b2,b3,b4,b5,b are in G.P. and a,c1,c2,c3,c4,c5,b are in H.P., then the roots of a3x2+b3x+c3=0 are
View Solution
