The perpenidicular drawn from the centre of a circle bisects any chord of the circle. The following are the steps involved in proving the above result. Arrange them in sequential order.
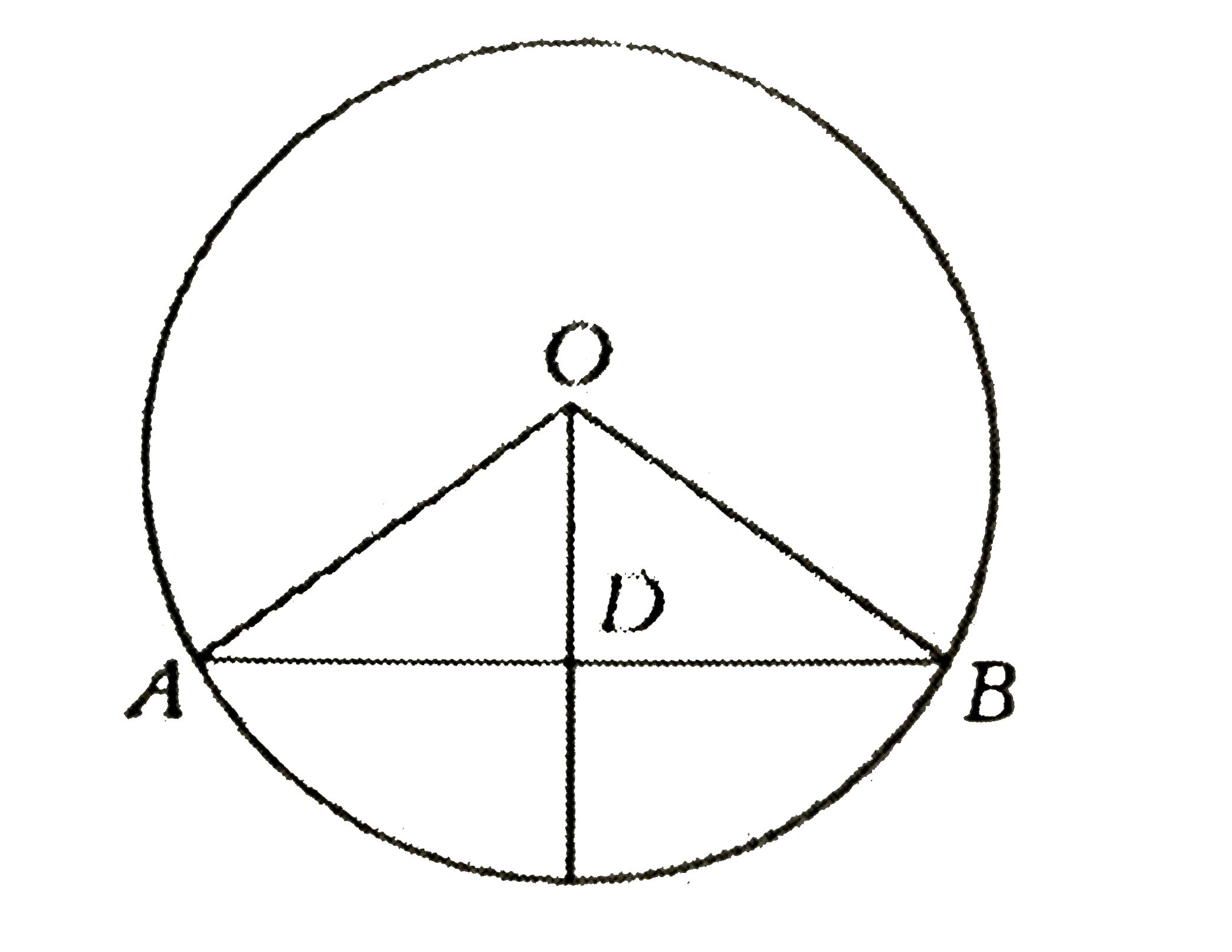
(A) Let ¯¯¯¯¯¯OD⊥¯¯¯¯¯¯AB .
(B) Let AB be the chord of the circle with centre O.
(C ) ΔODA≡ΔODB ( By RHS congruence property).
(D ) OA=OB (radii), OD=OD ( common side) and ∠ODA=∠ODB=90∘
(E ) AD=DB ( corresponding parts in congurents triangles ).
752 cu m
805 cu m
1016 cu m
1214 cu m
Step by step video & image solution for The perpenidicular drawn from the centre of a circle bisects any chord of the circle. The following are the steps involved in proving the above result. Arrange them in sequential order. (A) Let bar(OD) _|_ bar(AB) . (B) Let AB be the chord of the circle with centre O. (C ) Delta ODA -= Delta ODB ( By RHS congruence property). (D ) OA =OB (radii), OD= OD ( common side) and /_ ODA =/_ ODB =90^(@) (E ) AD=DB ( corresponding parts in congurents triangles ). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER 11Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 11Exercise:PART -B (SECTION-III)
Explore 8 Videos
- SAMPLE PAPER 11Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 11Exercise:PART -B (SECTION-IV)
Explore 9 Videos
- SAMPLE PAPER 11Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 11Exercise:PART -B (SECTION-V)
Explore 4 Videos
- SAMPLE PAPER 10 SOLVED Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 10 SOLVED Exercise:PART - B (SECTION - V)
Explore 4 Videos
- SAMPLE PAPER 11 (SELF - ASSESSMENT)Book:EDUCART PUBLICATIONChapter:SAMPLE PAPER 11 (SELF - ASSESSMENT)Exercise:SECTION -C
Explore 10 Videos
Similar Questions
The perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionThe perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionThe perpenidicular drawn from the centre of a circle bisects any chord of the circle. The following are the steps involved in proving the above result. Arrange them in sequential order.

(A) Let ¯¯¯¯¯¯OD⊥¯¯¯¯¯¯AB .
(B) Let AB be the chord of the circle with centre O.
(C ) ΔODA≡ΔODB ( By RHS congruence property).
(D ) OA=OB (radii), OD=OD ( common side) and ∠ODA=∠ODB=90∘
(E ) AD=DB ( corresponding parts in congurents triangles ).
View SolutionTheorem 10.3 : The perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionA line drawn drom the centre of a circle to a chord always bisects it. (True/False).
View SolutionProve that a diameter of a circle which bisects a chord of the circle also bisects the angle subtended by the chord at the centre of the circle.
View SolutionIf O is the centre of a circle with radius r and AB is a chord of the circle at a distance r2 from O, then ∠BAO=
View SolutionO is the centre of a circle of diameter AB. If chord AC= chord BC, then find the value of ∠ABC.
View SolutionTheorem :-2 The perpendicular from centre of a circle to the chord bisects the chord and Perpendicular bisectors of two chords of a circle intersects at the centre.
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View Solution