In the given figure, AC = 12 cm, AB = 3 cm and BC = 4 cm. Then cot θ = ?
To solve the problem, we need to find the value of cot θ in triangle ABC where AC = 12 cm, AB = 3 cm, and BC = 4 cm.
1. Identify the Triangle and Angles:
- We have triangle ABC where AC is the hypotenuse, AB is one leg, and BC is the other leg. We need to find cot θ, where θ is the angle at point B.
2. Recall the Definition of Cotangent:
- The cotangent of an angle in a right triangle is defined as the ratio of the length of the adjacent side (base) to the length of the opposite side (perpendicular).
- Mathematically, cot θ = base / perpendicular.
3. Identify the Base and Perpendicular:
- In respect to angle θ (angle B):
- The base (adjacent side) is BC.
- The perpendicular (opposite side) is AB.
4. Substitute the Values:
- From the problem, we know:
- BC = 4 cm (base)
- AB = 3 cm (perpendicular)
- Now substitute these values into the cotangent formula:
cot θ=BCAB=4 cm3 cm
5. Calculate cot θ:
- Therefore, cot θ = 43.
Final Answer:
cot θ=43
---
- We have triangle ABC where AC is the hypotenuse, AB is one leg, and BC is the other leg. We need to find cot θ, where θ is the angle at point B.
- The cotangent of an angle in a right triangle is defined as the ratio of the length of the adjacent side (base) to the length of the opposite side (perpendicular).
- Mathematically, cot θ = base / perpendicular.
- In respect to angle θ (angle B):
- The base (adjacent side) is BC.
- The perpendicular (opposite side) is AB.
- From the problem, we know:
- BC = 4 cm (base)
- AB = 3 cm (perpendicular)
- Now substitute these values into the cotangent formula:
cot θ=BCAB=4 cm3 cm
- Therefore, cot θ = 43.
cot θ=43
Topper's Solved these Questions
- SAMPLE PAPER SOLVED 4 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SOLVED 4 EXERCISE - SECTION - C
10 Videos
- SAMPLE PAPER SOLVED 4 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SOLVED 4 EXERCISE - SECTION - C
10 Videos
- SAMPLE PAPER SOLVED 9 BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SOLVED 9 EXERCISE - Part - B (Section -V)
4 Videos
- SAMPLE QUESTION PAPER 02BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE QUESTION PAPER 02EXERCISE - SECTION - D
9 Videos
Similar Questions
Knowledge Check
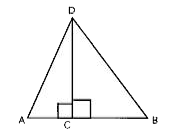
In the figure given below, AD = 4 cm, BD = 3 cm and CB = 12 cm, then cot θ equals:
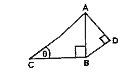 A34B512C43D125
A34B512C43D125In the given figure if DE∣∣BC, AD = 2.5 cm, DB = 3.5 cm and EC = 4.2 cm, then the measure of AC is:
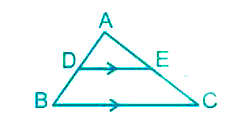 A(A). 3 cmB(B). 3.2 cmC(C). 7.2 cmD(D). 7.4 cm
A(A). 3 cmB(B). 3.2 cmC(C). 7.2 cmD(D). 7.4 cmIn the given figure AB = 12, AC = 15 cm and AD = 6 cm. BC∣∣DE, find the length of AE
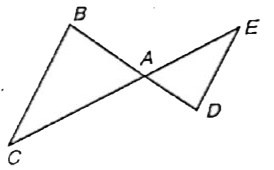 A6 cmB7.5 cmC9 cmD10 cm
A6 cmB7.5 cmC9 cmD10 cm
In the given figure AD = 4 cm BD = 3 cm and CB = 12 cm . Find the value of cot θ
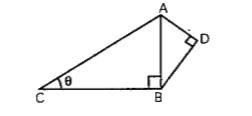
View SolutionIn the figure, AC = 3 cm, BC = 6 cm and CD = 4 cm. Write the value of (i) tan B (ii) cot A
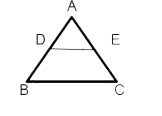
View SolutionIn the given figure, AD = 2cm, BD = 3 cm, AE = 3.5 cm and AC = 7 cm. Is DE parallel to BC ?
View SolutionIn a given figure, AB||CD||PQ, AB = 12 cm., CD = 18 cm. and AC = 6 cm. then value of PQ (in cm.) will be-
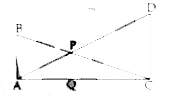
View SolutionIn the given figure, if AB = 10 cm, CD = 7 cm, SD = 4 cm and AS = 5 cm, then BC = ?

View Solution

