the corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
(2,0),(2019,4519),(0,3)
(0,3),(2019,4519),(0,5)
(2,0),(2019,4519),(5,0)
(0,0),(2,0),(2019,4519),(0,3)
The correct Answer is:C
To find the corner points of the feasible region defined by the system of linear inequalities:
1. Identify the inequalities:
- 3x+5y≤15
- 5x+2y≥10
- x≥0
- y≥0
2. Convert inequalities to equations:
- For 3x+5y=15
- For 5x+2y=10
3. Find the intercepts for the first equation 3x+5y=15:
- Set x=0:
3(0)+5y=15⟹y=3(Point: (0, 3))
- Set y=0:
3x+5(0)=15⟹x=5(Point: (5, 0))
4. Find the intercepts for the second equation 5x+2y=10:
- Set x=0:
5(0)+2y=10⟹y=5(Point: (0, 5))
- Set y=0:
5x+2(0)=10⟹x=2(Point: (2, 0))
5. Plot the lines:
- Plot the points (0, 3), (5, 0) for the line 3x+5y=15.
- Plot the points (0, 5), (2, 0) for the line 5x+2y=10.
6. Find the intersection of the two lines:
- Solve the equations simultaneously:
3x+5y=15(1)
5x+2y=10(2)
- From (1), express y:
5y=15−3x⟹y=15−3x5
- Substitute y in (2):
5x+2(15−3x5)=10
5x+30−6x5=10
25x+30−6x=50(Multiply through by 5)
19x=20⟹x=2019
- Substitute x back to find y:
y=15−3(2019)5=15−60195=285−60195=22519⋅5=4519
- Thus, the intersection point is (2019,4519).
7. Identify the corner points:
- The corner points of the feasible region are:
- (0, 3)
- (5, 0)
- (2, 0)
- (0, 5)
- (2019,4519)
8. Conclusion:
- The corner points of the feasible region are:
- (2, 0)
- (5, 0)
- (2019,4519)
- (0, 3)
Final Answer: The corner points are (2,0), (5,0), and (2019,4519).
- 3x+5y≤15
- 5x+2y≥10
- x≥0
- y≥0
- For 3x+5y=15
- For 5x+2y=10
- Set x=0:
3(0)+5y=15⟹y=3(Point: (0, 3))
- Set y=0:
3x+5(0)=15⟹x=5(Point: (5, 0))
- Set x=0:
5(0)+2y=10⟹y=5(Point: (0, 5))
- Set y=0:
5x+2(0)=10⟹x=2(Point: (2, 0))
- Plot the points (0, 3), (5, 0) for the line 3x+5y=15.
- Plot the points (0, 5), (2, 0) for the line 5x+2y=10.
- Solve the equations simultaneously:
3x+5y=15(1)
5x+2y=10(2)
- From (1), express y:
5y=15−3x⟹y=15−3x5
- Substitute y in (2):
5x+2(15−3x5)=10
5x+30−6x5=10
25x+30−6x=50(Multiply through by 5)
19x=20⟹x=2019
- Substitute x back to find y:
y=15−3(2019)5=15−60195=285−60195=22519⋅5=4519
- Thus, the intersection point is (2019,4519).
- The corner points of the feasible region are:
- (0, 3)
- (5, 0)
- (2, 0)
- (0, 5)
- (2019,4519)
- The corner points of the feasible region are:
- (2, 0)
- (5, 0)
- (2019,4519)
- (0, 3)
Topper's Solved these Questions
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION - C
9 Videos
- SAMPLE PAPER 8BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - SECTION - C
9 Videos
- CBSE TERM -1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM -1 SAMPLE PAPER 1EXERCISE - SECTION - C
4 Videos
Similar Questions
Knowledge Check
The graphical solution of the system of linear inequalities 3x,4y≥12,y≥1,x≥0 is
A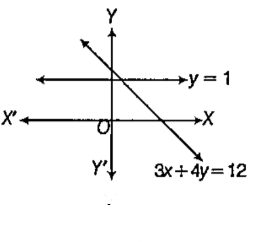 B
B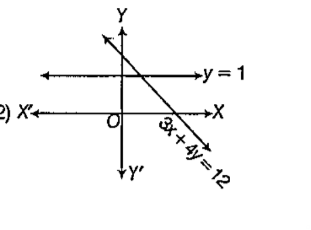 C
C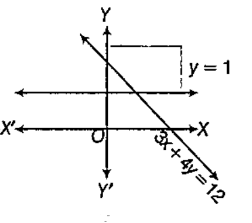 D
D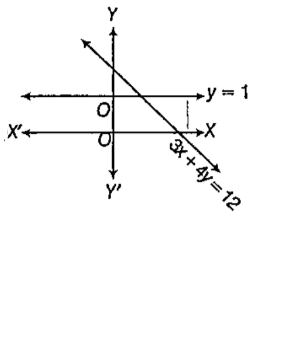
x+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View Solution3x+2y≤150,x+4y≤80,x≤15,y≥0,x≥0
View Solutionx+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View Solutionx+y≤10,4x+3y≤24,x≥,x≥0,y≥0
View Solution3x+4y≤60,x≥2y,x≥1,y≥0
View SolutionZ=3x+2y
x+2y≤10,3x+y≤15,x≥0,y≥0
View SolutionSolve the following system of linear inequalities
3x+2y≥24,3x+y≤15,x≥4.
View Solution