Assertion (A): Where magnetic flux changes, emf is induced. Reason (R): Line integral of induced electric field around the closed loop is non zero.
Both (A) and (R) are true and (R) is the correct explanation of (A).
Both (A) and (R) are true but (R) is not the correct explanation of (A)
is true but (R) is false.
(A) is false and (R) is also false
To analyze the assertion and reason provided in the question, we will break down the concepts involved step by step.
Step 1: Understanding the Assertion
Assertion (A): Where magnetic flux changes, emf is induced.
- According to Faraday's law of electromagnetic induction, a change in magnetic flux through a closed loop induces an electromotive force (emf) in that loop. This is a fundamental principle in electromagnetism.
Step 2: Understanding the Reason
Reason (R): Line integral of induced electric field around the closed loop is non-zero.
- Faraday's law can be mathematically expressed as:
∮E⋅dl=−dΦBdt
where E is the induced electric field, dl is an infinitesimal length element along the closed loop, and ΦB is the magnetic flux. The negative sign indicates that the induced emf opposes the change in magnetic flux (Lenz's Law).
- If the magnetic flux is changing, then dΦBdt≠0, which implies that the line integral ∮E⋅dl must also be non-zero. This indicates that the electric field induced is non-conservative, which is a characteristic of fields generated by changing magnetic fields.
Step 3: Conclusion
- Since both the assertion and the reason are true and the reason correctly explains the assertion, we can conclude that the assertion (A) is true and the reason (R) is true, and R is the correct explanation of A.
Final Answer
- Both Assertion (A) and Reason (R) are true, and R is the correct explanation of A.
---
Assertion (A): Where magnetic flux changes, emf is induced.
Step 2: Understanding the Reason
Reason (R): Line integral of induced electric field around the closed loop is non-zero.
∮E⋅dl=−dΦBdt
where E is the induced electric field, dl is an infinitesimal length element along the closed loop, and ΦB is the magnetic flux. The negative sign indicates that the induced emf opposes the change in magnetic flux (Lenz's Law).
- If the magnetic flux is changing, then dΦBdt≠0, which implies that the line integral ∮E⋅dl must also be non-zero. This indicates that the electric field induced is non-conservative, which is a characteristic of fields generated by changing magnetic fields.
- Since both the assertion and the reason are true and the reason correctly explains the assertion, we can conclude that the assertion (A) is true and the reason (R) is true, and R is the correct explanation of A.
- Both Assertion (A) and Reason (R) are true, and R is the correct explanation of A.
Topper's Solved these Questions
- SAMPLE PAPER SELF-ASSESSMENT (11)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF-ASSESSMENT (11)EXERCISE - SECTION -C
1 Videos
- SAMPLE PAPER SELF-ASSESSMENT (11)BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF-ASSESSMENT (11)EXERCISE - SECTION -C
1 Videos
- CBSE TERM-1 SAMPLE PAPER 1BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 1EXERCISE - SECTION-C
6 Videos
Similar Questions
Knowledge Check
Assertion : An emf →E is induced in a closed loop where magnetic flux is varied. The induced →E is not a conservative field.
Reason : The line intergral →E.→dl around the closed loop is non-zero.AIf both Assertion & Reason are true and the reason is the correct explanation of the assertion.Bif both assertion and reason are true but reason is not the correct expalanation of the assertionCif assertion is true , but reason is falseDboth assertion and reason are false statements.Assertion (A) : A changing magnetic flux may produce an induced emf.
Reason (R) : Faraday experimentally demonstrated the induced emf.AIf both assertion and reason are true and the reason is the correct explanation of the assertion.BIf both assertion and reason are true but reason is not the correct explanation of the assertion.CIf assertion is true but reason is falseDIf the assertion is false but reason is true.Consider a conducting circular loop placed in a magentic filed as shown. When magnetic field changes with time, magentic flux also changes and emf is induced.
e=−dϕdt
If resistance of loop is R then induced current.
i=eR
For Current, charge must have come into motion. Magnetic force cannot make the statinoary charges to move. Actually there is an induced electric field in the conductor caused by changing magnetic flux, which make the change to move
∫→E.d→l=e=−dϕdt
This induced electric field is non-electrostatic by nature. line integral of →E around a closed path is non-zero

A square non- conducting loop 20 cm on a side is placed in a magnetic field The centre of side AB coincides with the centre of magnetic field The magnetic field is increasing at the rate of 2T/s. Find the magnitude of line integral of induced electric field along path BC.
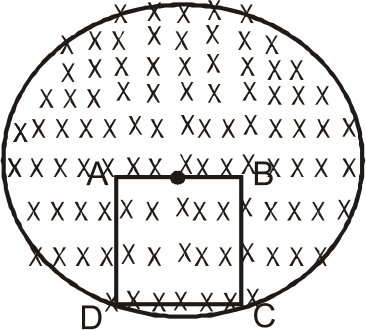 A10 mVB20 mVC30 mVDzero
A10 mVB20 mVC30 mVDzero
Assertion (A): Whenever the magnetic flux linked with a closed coil changes there will be an induced emf as well as an induced current.
Reason (R ) : Accroding to Faraday, the induced emf is inversely proportional to the rate of change of magnetic flux linked with a coil.
View SolutionA: The electric field induced due to changing magnetic field is non-conservative,
R: The line integral of the electric field induced due to changing magnetic field along a closed loop is always zero.
View SolutionAsseration: Magnetic flux linked to closed surface is zero.
Reason: Direction of induced current due to change of magnetic flux is given by faraday's law.
View SolutionThe magnetic flux linked with a coil is ϕ and the emf induced in it is e.
View SolutionAsseraton: The work done by a charge in a closed (induced) current carrying loop is non-zero.
Reason: Induced electric field is non-conservative in nature.
View Solution
