If two chords having lengths a2−1 and 3(a+1), where a is a constant of a circle bisect each other, then the radius of the circle is
6
15/2
8
19/2
The correct Answer is:B
Similar Questions
Which of the following statements are true and which have are false? In each case give a valid reason for saying so p: Each radius of as circle is a chord of the circle q: The centre of a circle bisects each chord of the circle.
View SolutionWhich of the following statements are true and which have are false? In each case give a valid reason for saying so p: Each radius of as circle is a chord of the circle q: The centre of a circle bisects each chord of the circle.
View Solution
Knowledge Check
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
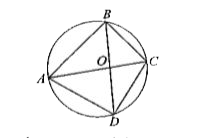 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogramTwo chords of a circle, of lengths 2a and 2b are mutually perpendicular. If the distance of the point, at which the chords interect, from the centre of the circle is c (c < radius of the circle), then the radius of the circle is :
A√a2+b2+c22B√abcCa + b - cD√a2+b2−c22Give two circles intersecting orthogonally having the length of common chord 24/5 units. The radius of one of the circles is 3 units.
The radius of other circle isA6 unitsB4 unitsC2 unitsD4units
If radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is
View SolutionIf two equal circles are such that the centre of one lies on e circumference of the other, then the ratio of the common chord of two circles to the radius of any of the circles is :
View SolutionIf radii of two concentric circles are 4 cm and 5 cm, then length of each chord of one circle which is tangent to the other circle, is
View SolutionIf radii of two concentric circles are 4 cm and 5 cm Then the length of the chord of one circle which is tangent to the other circle is
View SolutionIf two equal circles are such that the centre of one lies on e circumference of the other, then the ratio of the common chord of two circles to the radius of any of the circles is :
View Solution
