If V1 and V2 are subspace of R4 given by
V1={(a,b,c,d):b−2c+d=0}
V2={(a,b,c,d):a=d,b=2c}
the dimension of V1 is 1
the dimension of V2 is 2
the dimension of V1 is 4
the dimension of V2 is 3
The correct Answer is:B
Similar Questions
Knowledge Check
The cycle is shown in figure is made of one mole of perfect gas in a cylinder with a piston . The processes A to B and C to D are isochoric wheras process B to C and D to A are adiabatic, the work done in one cycle is (VA=VB=V,VC=VD=2Vand γ=5/3)
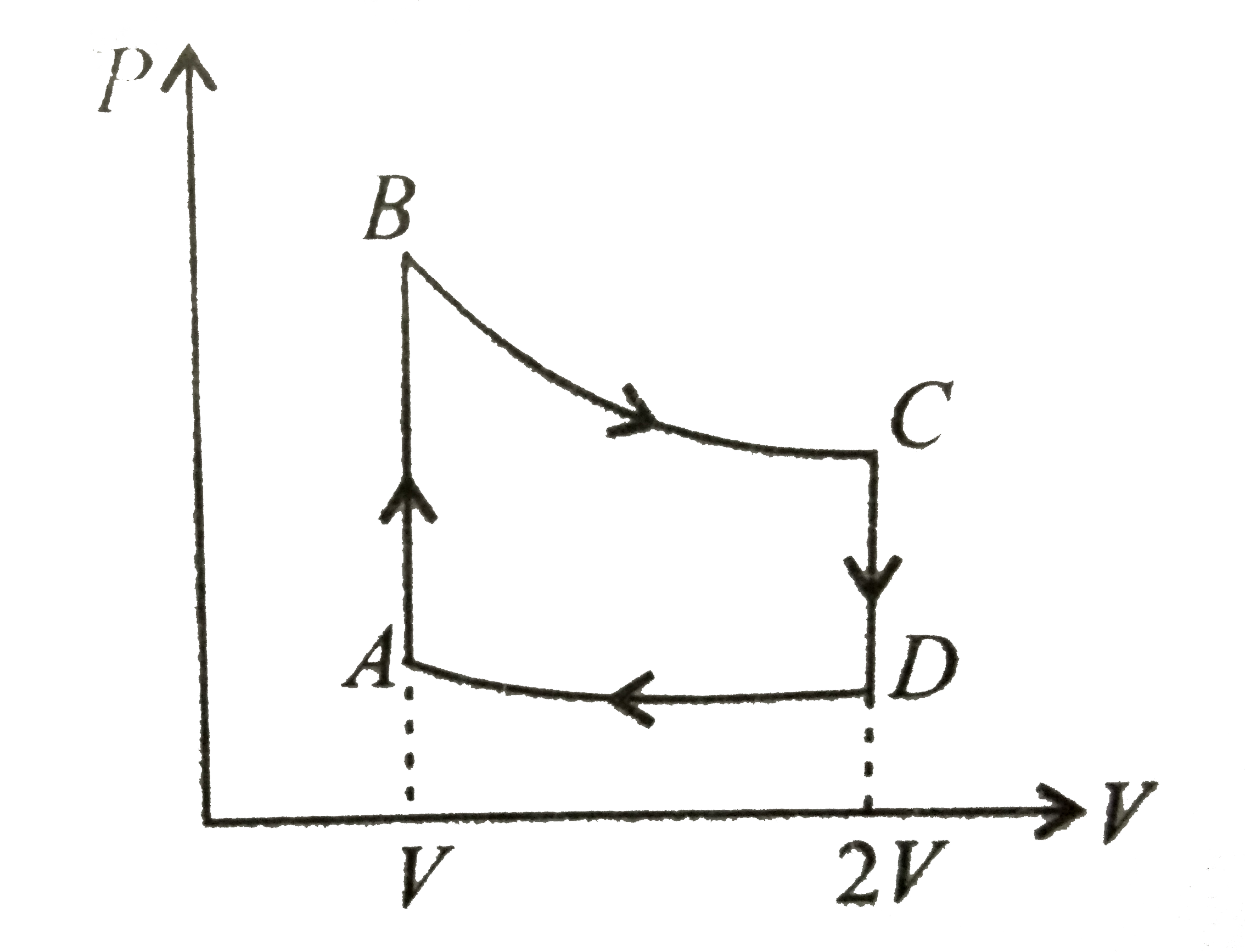 A[1−432](PB−PA)VB32[1−323](PB−PA)VC32[1−2−23](PB−PA)VD52[1−2−23](PB−PA)V
A[1−432](PB−PA)VB32[1−323](PB−PA)VC32[1−2−23](PB−PA)VD52[1−2−23](PB−PA)VThe cycle is shown in figure is made of one mole of perfect gas in a cylinder with a piston . The processes A to B and C to D are isochoric whereas process B to C and D to A are adiabatic, the work done in one cycle is (VA=VB=V,VC=VD=2Vand γ=5/3)
 A[1−432](PB−PA)VB32[1−323](PB−PA)VC32[1−2−23](PB−PA)VD52[1−2−23](PB−PA)V
A[1−432](PB−PA)VB32[1−323](PB−PA)VC32[1−2−23](PB−PA)VD52[1−2−23](PB−PA)VLet a, b and c be three non-zero and non-coplanar vectors and p, q and r be three given by →p=→a+→b−2→c,→q=3→a−2→b+→c and r=→a−4→b+2→c. If the volume of the parallelopiped determined by→a,→band→c is V1 and that of the parallelopiped determined by →p,→qand→r is V2, then V2:V1=
A2:3B5:7C15:1D1:1
Let →a,→b,and→c be non-zero vectors and →V1=→a×(→b×→c)and→V2=(→a×→b)×→c. Vectors →V1and→V2 are equal. Then (a).→aan→b are orthogonal (b). →aand→c are collinear (c). →band→c are orthogonal (d). →b=λ(→a×→c)whenλ is a scalar
View Solutiona, b are the real roots of x2+ px +1-0 and c, d are the real roots of 2 x + qx + 1 = 0 then (a-c)(h-c)(a + d)(b + d) is divisible by n) a+b+c+d (b) a +b-c-d (d) a -b-c-d (c) a-b+c-d
View SolutionV1, V2, V3 and V4 are the volumes of four cubes of side lengths x cm , 2x cm , 3x cm and 4x cm respectively. Some statements regarding these volumes are given below V1+V2+2V3<V4 (2) V1+4V2+V3<V4 (3) 2(V1+V3)+V2=V4 Which of these statements are correct? (a) 1 and 2 (b) 2 and 3 (c) 1 and 3 (d) 1, 2 and 3
View Solutionmatch the columns
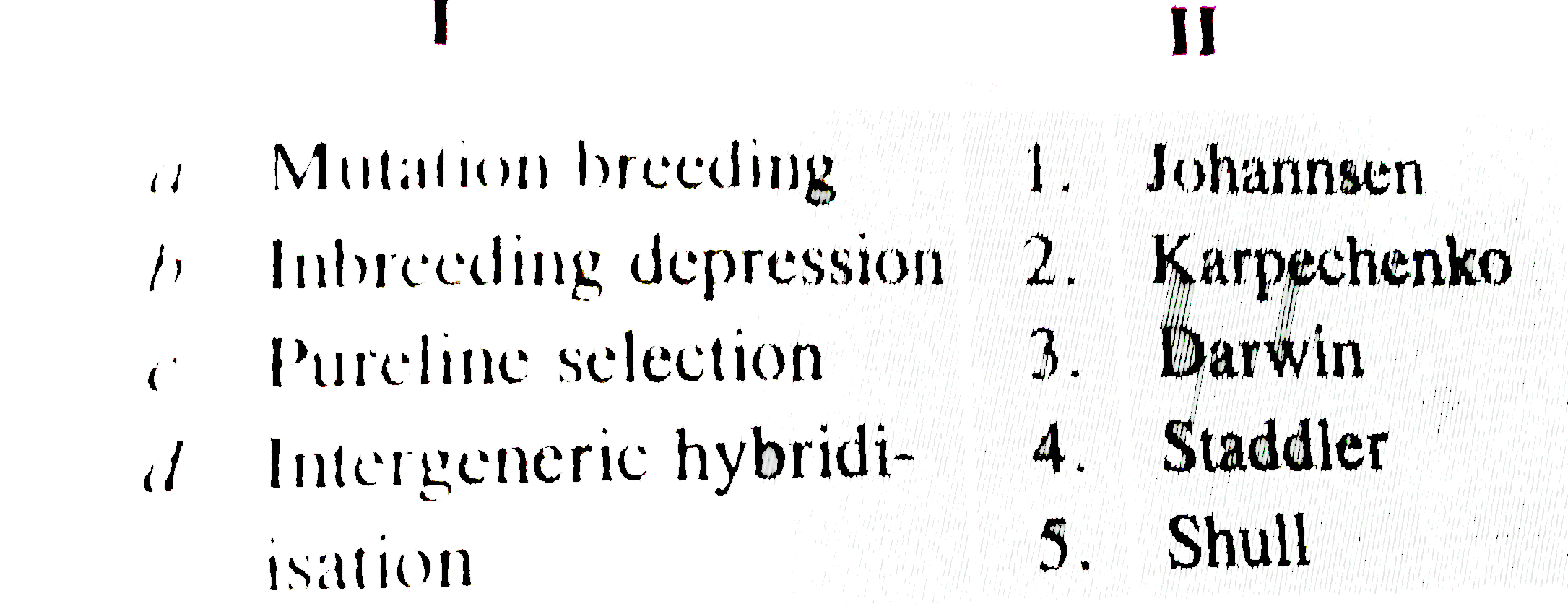
(a) a -4, b-2,c-5,d-1
(b) a-4,b-5,c-2,d-1
(c) a-4,b-5,c-1,d-2
(d) a-5, b-4,c-1,d-2
View SolutionIf a>0 and discriminant of ax2+2bx+c is negative, then ∣∣ ∣∣abax+bbcbx+cax+bbx+c0∣∣ ∣∣ is a.+ve b. (ac−b)2(ax2+2bx+c) c. −ve d. 0
View Solution
