A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec Solution in Telugu
Step by step video & image solution for A particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s= f(t)=8t+t^3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - MEAN VALUE THEOREM (VERY SHORT ANSWER TYPE QUESTIONS)
7 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - MAXIMA & MINIMA (LONG ANSWER TYPE QUESTIONS)
8 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - TANGENTS & NORMALS (LONG ANSWER TYPE QUESTIONS)
9 Videos
- MODEL PAPER 9BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 9EXERCISE - SECTION C (Long answer type questions)
7 Videos
Similar Questions
Define Rolles mean value theorem.
View SolutionThe sum of two numbers is 16. Find the numbers so that the sum of square is minimum.
View SolutionIF the tangent at a point on the curve x2/3+y2/3=a2/3 intersects the coordinate axes in A and B then show that the length AB is a constant.
View SolutionIf f:A→B is a bijective function then prove that
(ii) f−1of=IA.
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View Solutionसरल रेखा में गतिमान एक कण का त्वरण (a) समय (t) ग्राफ संलग्न चित्र में प्रदर्शित है। कण का प्रारम्भिक वेग 2 मीटर/सेकण्ड है। ज्ञात कीजिए (i) t=3 सेकण्ड तथा t=6 सेकण्ड पर कण का वेग (ii) t=0 से t=6 सेकण्ड के बीच कण का औसत त्वरण।
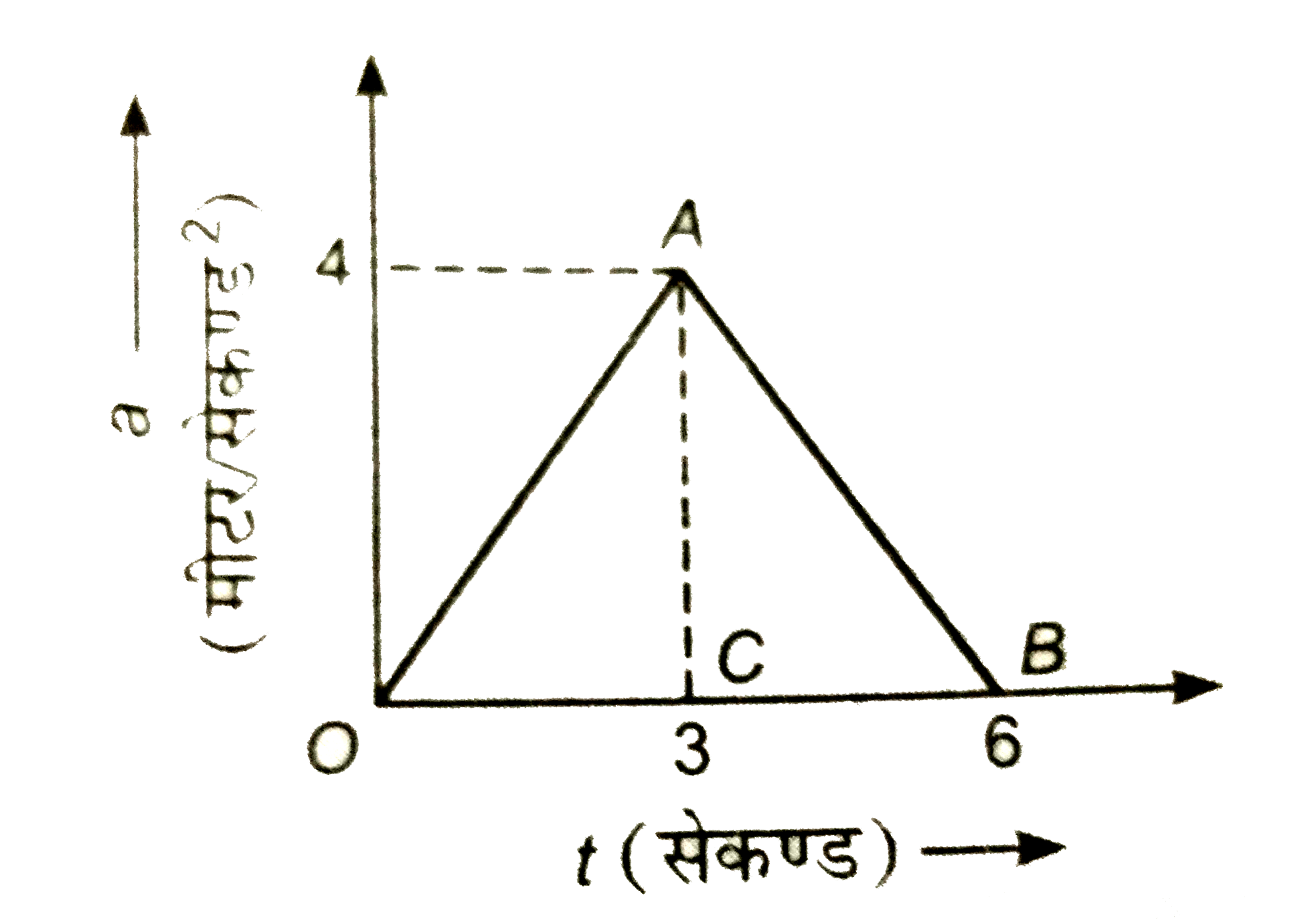
View SolutionThe acceleration of a particle moving along a straight line is (6t2−3t)cm/s2, at time t seconds. If the velocity of the particel at time 2 seconds be 10cm/s, find its velocity at time t seconds.
View Solutionएक कण एक सरल रेखा में इस तरह से चलता हैं ताकि इसका स्थिति t सेकेण्ड के बाद s(t)=6t−t2 हैं | इसका प्रारंभिक वेग क्या हैं।
View SolutionA particle is moving in a straight line so that after 't' seconds its distance is 'S' (in cms) from a fixed point of the line is given be S=f(t)=8t+t3.
Find (i) the velocity at time t=2 (ii) the initial velocity (iii) acceleration at t=2 sec
View SolutionA particle is moving in a straight line and its distance x cm from a fixed point on the line at any time t seconds is given by ,
x=112t4−23t3+32t2+t+15.
At what time is the velocity minimum ? Also find the minimum velocity.
View SolutionAt time t, the distance s of a particle moving in a straight line is given by s=4t2+2t. Find the average velocity between t= 2sec and t= 8 sec.
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line so that after t seconds its distance is s (in cms) from a fixed point on the line is given by s=f(t)=8t+t3. Find the velocity at time t= 2sec (ii) the initial velocity can acceleration at t=2 sec
View SolutionA particle is moving in a straight line with initial velocity u and uniform acceleration f . If the sum of the distances travelled in t^(th) and (t + 1)^(th) seconds is 100 cm , then its velocity after t seconds, in cm//s , is.
View SolutionA particle is moving in a straight line is at a distance S from a point O on the line in time t, where S=t3−6t2+8t+5.Find the velocity when the acceleration is 12cm/sec2.
View SolutionA particle is moving along a line according s= f(t) = 8t + t^3 . Find the initial velocity
View Solution
