Find the constant C, so that
F(x)=C(23)x,x=1,2,3……………… is the p.d.f of a discrete random variable X. Solution in Telugu
Step by step video & image solution for Find the constant C, so that F(x)=C((2)/(3))^(x),x=1,2,3……………… is the p.d.f of a discrete random variable X. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - RANDOM VARIABLES & PROBABILITY DISTRIBUTIONS (LONG ANSWER TYPE QUESTIONS)
6 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - CIRCLES(VERY SHORT ANSWER TYPE QUESTIONS)
14 Videos
- MOST IMPORTANT QUESTIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MOST IMPORTANT QUESTIONSEXERCISE - PROBABILITY (LONG ANSWER TYPE QUESTIONS)
6 Videos
- MODEL PAPER 9 BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 9 EXERCISE - SECTION-C (III. LONG ANSWER TYPE QUESTIONS)
7 Videos
Similar Questions
The probability distribution of a random variable X is given below.
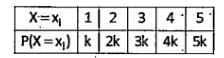
Find the value of k, mean, also find variance of X.
View SolutionFind the centre and radius of the circle x2+y2+6x+8y−96=0.
View SolutionState and prove addition theorem on probability.
View SolutionIf n is a positive integer, show that
(P+iQ)1/n+(P−iQ)1/n=2(P2+Q2)1/2ncos(1n,tan.QP).
View SolutionIf the probability mass function of a discrete random variable X is P(x)=Cx3,x=1,2,3=0, otherwise. Then, E(X) is equal to
View SolutionFind k, if the function f defined by f(x)=kx,0<x<2 =0 , otherwise is the p.d.f of a random variable X.
View SolutionThe p.d.f of a random variable X is given by f(x)=3(1−2x2),0<x<1
= 0 , otherwise
Find P(14<X<13)
View SolutionThe p.d.f of a continuous random variable X is f(x)=x23,−1<x<2 0 = otherwise Then the c.d.f of X is
View SolutionFind the constant C, so that
F(x)=C(23)x,x=1,2,3……………… is the p.d.f of a discrete random variable X.
View SolutionThe p.d.f. of a random variable X is
(f)x=2x,0≤x≤1
=0, otherwise
Then the value of P(13<X<12) is
View SolutionIf the probability mass function of a discrete random variable X is
P(x)=Cx3,x=1,2,3
=0, otherwise
Then E(X)=
View SolutionIf the p.d.f of a random variable X is given by f(x)=2x9,0<x<3, then find E(3X+8).
View SolutionIf a continuous random variable X has the p.d.f. f(x)=4k(x−1)31≤x≤3, then find P(1≤X≤2).
View Solutionrandom variable X has the range {1,2,3,……….}. If P(X=r)=cr/r for r=1,2,3,……… then c=
View SolutionThe range of a random variable X={1,2,3,…………..) and the probabilities are given by
P(X=k)=3ckk!(k=1,2,3,………..) and c is a constant . Then c=
View SolutionA continuous random variable x has the p.d.f defined by f(x) = {Ce−ax0<x<∞0elsewhere find the value of C if a>0.
View Solution
