Question

State and prove law of conservation of energy in case of a freely falling body.
A pump is required to lift 600 kg of water per minute from a well 25 m'deep and to eject it with a speed of $50m{s}^{-1}$ Calculate the power required to perform the above task.

Explanation

Law of conservation of energy : Energy can neither be created nor destroyed .But it can be converted from one form into the another form so that the total energy will remains constant in a closed system.
Proof : In case of a freely falling body :
Let a body of mass is dropped from a height .H. at point A . Forces due to gravitational field are conservative forces . so total mechanical energy (E=P.E+K.E.) is constant i.e ., neither destroyed nor created.

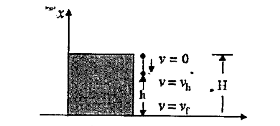
(1) At point H: Velocity of body `v=0rArrK=0`
Potential energy (u) = mgH
where H= height above the ground
`T.E=u+K=mgH` .......(1)
2. At point ) , i.e ., just before touching the ground : `T.E=u+K=mgH` .......(1)
2. At point 0 , i.e ., just before touching the ground :
A constant force is a sepcial case of specially dependent force F(x) so mechanical energy is conserved.
So energy at H= Energy is conserved .
So energy at H= Energy at 0 = mgH
Proof : At point .0. height `=0rArrv=sqrt(2gH),u=0`
`K_(0)=(1)/(2)mv^(2)=(1)/(2)m2gH=mgH`
Total energy E= mgH+0=mgH......(2)
3. At any point h: Let height above ground =h
`u=mgh,K_(h)=(1)/(2)mV^(2)`
where `V=sqrt(2g(h-x))`
`therefore` Velocity of the body when it falls through a height (h-x) is
`sqrt(2g(h-x))`
`therefore`Total energy at any point is constant .
Hence . law of conservation of energy is proved.
Conditions to apply law of conservation of energy :
(1) Work done by interbal forces is conservative . When the above two conditions are satisfied then total me chanical energy of a system will remain constant .
Mass of water m= 600 kg , depth = h= 25 m
Speed of water `v=25m//s,g=10m//s^(2)`, time t=1 min =60 sec.
Power of motor P= Power to lift water `(P_(1))` +Kinetic energy of water (K.E) per second.
Power to lift water `P_(1)=(mgh)/(t)=(""^(10)cancel600xx10xx25)/(cancel60)=2500` watt.
K.E . of water per second `=(1)/(2)(mv^(2))/(t)`
`=(1)/(2)(""^(10)cancel600xx25xx25)/(cancel(60))=(6250)/(2)=3125` watt.
`therefore` Power of motor P=2500+3125=5625watt =5.625K.W.