Define vector product. Explain the properties of a vector product with two examples.

Text Solution
Verified by Experts

Vector product or cross product : If the product of two vectors (say ¯¯¯Aand¯¯¯B) gives a vector then that multiplication of vectors is cross product or vector product of vectors.
Mathematically ¯¯¯Aׯ¯¯B=∣∣¯¯¯A∣∣∣∣¯¯¯B∣∣sinθ.ˆn
Vector product is a unit vector perpendicular to both ¯¯¯Aand¯¯¯B or perpendicular to the plane of ¯¯¯Aand¯¯¯B.
Properties of cross product :
1. Cross product is not commutative i.e. ¯¯¯Aׯ¯¯B≠¯¯¯Bׯ¯¯A. But ¯¯¯Aׯ¯¯B=−¯¯¯Bׯ¯¯A
2. Cross product obeys distributive law i.e. ¯¯¯A×(¯¯¯B+¯¯¯C)=(¯¯¯Aׯ¯¯B)+(¯¯¯Aׯ¯¯C)
3. If any vector is represented by the combination of ¯i,¯jand¯k then cross product will obey right hand screw rule.
4. The product of two coplanar perpendicular unit vectors will generate a unit vector perpendicular to that plane i.e., ¯iׯj=¯k,¯jׯk=¯iand¯kׯi=¯j
5. Cross product of parallel vectors is zero i.e. ¯iׯi=¯jׯj=¯kׯk=0
Examples of cross product :
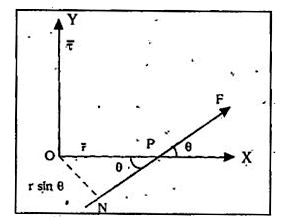
1. Torque or moment of force (¯τ) : Torque is defined as the product of force and perpendicular distance from the point of application.
Let a force ¯¯¯F act on a point P which is at a distance .r. from .O.. Let the Force ¯¯¯F act with some angle .θ.on¯¯¯¯¯¯OP
The perpendicular distance ON = ¯rsinθ
∴ Torque τ=¯rׯ¯¯F
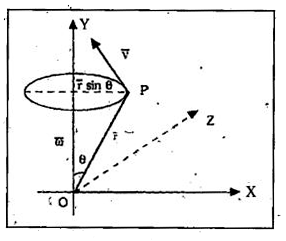
ocr_image
2. Angular momentum and angular velocity : Let a rigid body is rotating about the Y-axis with a constant angular velocity .ω. Consider a point .P. in the body which is at a distance ¯r from origin.
The velocity ¯v is perpendicular to both ¯¯ωand¯¯¯P
Velocity ¯v=→ω¯rsinθ
∴ Velocity ¯v=¯¯ωׯr
(OR) Angular momentum (¯¯¯L) = radius (¯r)× momentum (¯¯¯P)
∴ Angular momentum (¯¯¯L)=¯r×(m¯v)=m(¯rׯv)
ocr_image

Updated on:21/07/2023
Doubtnut Promotions Banner
|