What are collisions ? Explain the possible types of collisions ?
Develop the theory of one dimensional elastic collision.
To simulate car accidents, auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car-of mass 1000 kg moving with a speed 18.0 km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−7. What is the maximum compression of the spring ?
A process in which the motion of a system of particles changes but keeping the total momentum conserved is called collision. Collisions are two types : 1) elastic 2) inelastic.
Velocities of two bodies after elastic collision :
Let two bodies of masses m1,m2 , are moving with velocities u1,u2 alono the came line in came direction collided elastically.
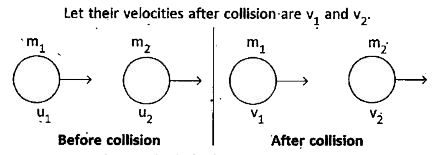
After collision According to the law of conservation of linear, momentum
m1u1+m2u2=m1v1+m2v2
or m1(u1−v1)=m2(v2−u2) .......(1)
According to the law of conservation of kinetic energy
12m1u21+12m2u22=12m1v21+12m2v22
m1(u21−v21)=m2(v22−u22) ....(2)
Dividing eqn. ( 2 ) by (1)
u21−v21u1−v1=v22−u22v2−u2 or u1+v1=v2+u2
u1−u2=v2−v1 ...(3)
i.e., In elastic collisions relative velocity of approach of the two bodies before collision = relative velocity of separation of the two bodies after collision.
To find v1, put v2=u1−u2+v1 in eqn. (1).
m2u1+m2u2=m1v1+m2(u1−u2+v1)
m1u1+m2u2=m1v1+m2u1−m2u2+m2v1
m1u1+m2u2−m2u1+m2u2=v1(m1+m2)
u1(m1−m2)+2m2u2=v1(m1+m2)
∴v1=m1−m2m1+m2u1+2m2m1+m2u2 ....(4)
Similarly, v2=u2(m2−m1)m1+m2+2m1u1m1+m2 .....(5)
Problem:
At maximum compression the kinetic energy of the car is converted entirely into the potential energy of the spring.
The kinetic energy of the moving car is
K=12mv2=12×103×5×5
K=1.25×104J
where we have converted 18km h−1 to 5ms−2 [It is useful to remember that 36km h−1=10ms−1].
At maximum compression Xm, the potential energy V of the spring is equal to the kinetic energy K of the moving car from the principle of conservation of mechanical energy.
V=12kx2m=1.25×104J
We obtain Xm=2.00m
We note that we have idealised the situation. The spring is considered to be massless. The surface has been considered to possess negligible friction.
Topper's Solved these Questions
- MODEL PAPER 12BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 12EXERCISE - SECTION - B
8 Videos
- MODEL PAPER 11BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 11EXERCISE - Section - C
3 Videos
- MODEL PAPER 13BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - MODEL PAPER 13EXERCISE - SECTION - C
4 Videos
Similar Questions
To stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of 18.0km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. What is the maximum compression of the spring?
View SolutionTo stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of 18.0km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. What is the maximum compression of the spring?
View Solution
Knowledge Check
A car of mass 1000 kg moving with a speed 18kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. The maximum compression of the spring is
A1 mB2 mC3 mD4 mA car of mass 1000 kg moving with a speed 18kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. The maximum compression of the spring is
A1 mB2 mC3 mD4 mA ball of mass m moving with speed v0 strikes a block of mass 3m kept at rest. The collision is completely inelastic . If k is spring constant , the maximum compression of the spring is
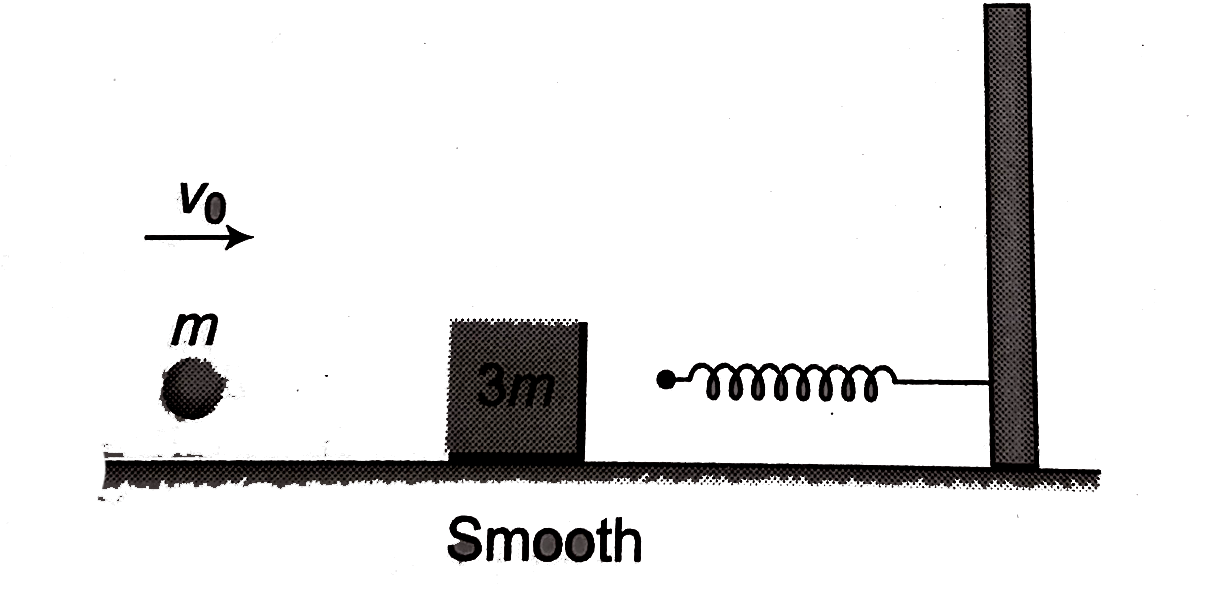 A√mv20kB√mv202kC√mv203kD√mv204k
A√mv20kB√mv202kC√mv203kD√mv204k
To stimulat car accidents, the auto manufacturers study the collisions of moving cars with mounted springs of different spring constants. Consider a typical simulation with a car of mass 1000kg moving with a speed of 18.0km/h on a smooth road and colliding with a horizontally mounted spring of spring constant 6.25×103Nm−1. What is the maximum compression of the spring?
View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View SolutionAuto manufactures study the collision of cars with mounted spring of different spring constant. Consider a car of mass 1500 kg moving with a speed of 36kmh−1 on a smooth road and colliding with a horizontally mounted spring of spring constant 7.5×103Nm−1. Find the maximum compression of the spring .
View SolutionTo simulate car accidents auto manufactures study the collisions of moving cars with mounted springs of different spring constants . Consider a typical simulation car of mass 1000 kg moving with a speed 18.0 km h −1 on a smooth road and colliding 6.25×103Nm−1 . What is the maximum compression of the spring ?
View Solution
