If the distance between the virtual image from Its real object is 60 cm in case of a concave mirror . The focal length of the concave mirror If the image formed is 3 times magnified image is

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:22.5

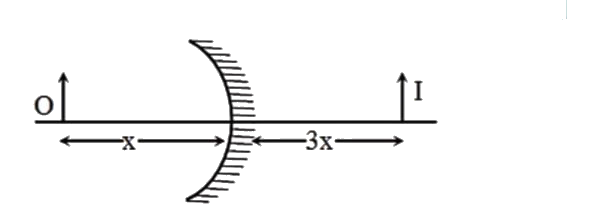
ocr_image
x=3x=60⇒x=15cm
u=−15cm
m=+3
∴m=ff−u⇒+3=ff−(−15)
∴3f+45=f⇒f=−22.5cm
|f|=22.5cm

Updated on:21/07/2023
|
Class 12PHYSICSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Object is placed 15 cm from a concave mirror of focal length 10 cm, then the nature of the image formed will be

    Amagnified and inverted
    Bmagnified and erect
    Csmall in size and inverted
    Dsmall in size and erect

  • An object is placed 40 cm from the concave mirror with a focal length of 20 cm . The image formed is :

    Abehind the mirror
    Bbetween the mirror and focus
    Cat focus
    Dcentre of curvature of mirror

  • An object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is

    AReal, inverted and same in size
    BReal, inverted and smaller
    CVirtual, erect and larger
    DVirtual, erect and smaller