A spherically symmetric gravitational system of particles has a mass density where is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce form the centre of the system is represented by


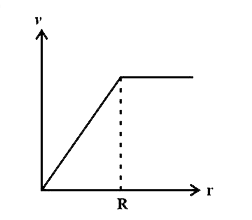
The correct Answer is:B
If Mis the total mass of the system of particles, then similar to a satellite revolving around the earth, the orbital velocity of the test mass is given by
For
i.e v or v r
i.e v Increases linearly with r up to r = R
Thus (1) and (4) are wrong but (2) and (3) satisfy this
For or
Thus Is correctly shown in figure (2). Figure (3) Is wrong because for r R, vis shown as constant.
Topper's Solved these Questions
Similar Questions
The density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View Solution
Knowledge Check
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A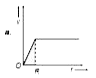 B
B C
C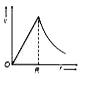 D
D
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A B
B C
C D
D
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A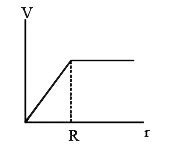 B
B C
C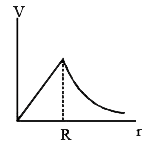 D
D
Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of raduis R? (r is measured from the centre of the spherical shell).
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View SolutionThree particles of equal mass M each are moving on a circular path with radius r under their mutual gravitational attraction. The speed of each particle is
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View SolutionA solid sphere of radius R has a volume charge density ρ=ρ0r2 (where ρ0 is a constant ans r is the distance from centre). At a distance x from its centre (for x<R), the electric field is directly proportional to :
View Solution
