Find the co-ordinates of the point which divides the line segment joining the points (4,-3) and (8,5) in the ratio 1:3 internally
(-5,-1)
(5,1)
(-1,5)
(5,-1)
To find the coordinates of the point that divides the line segment joining the points (4, -3) and (8, 5) in the ratio 1:3 internally, we can use the section formula. The section formula states that if a point divides the line segment joining two points (x1, y1) and (x2, y2) in the ratio m1:m2, then the coordinates (x, y) of the dividing point can be calculated as follows:
x=m1⋅x2+m2⋅x1m1+m2
y=m1⋅y2+m2⋅y1m1+m2
1. Identify the Points and the Ratio:
- Let point A = (4, -3) which is (x1, y1)
- Let point B = (8, 5) which is (x2, y2)
- The ratio m1:m2 = 1:3, where m1 = 1 and m2 = 3.
2. Calculate the x-coordinate:
- Using the formula for x:
x=m1⋅x2+m2⋅x1m1+m2
- Substitute the values:
x=1⋅8+3⋅41+3=8+124=204=5
3. Calculate the y-coordinate:
- Using the formula for y:
y=m1⋅y2+m2⋅y1m1+m2
- Substitute the values:
y=1⋅5+3⋅(−3)1+3=5−94=−44=−1
4. Combine the Coordinates:
- The coordinates of the point that divides the line segment in the ratio 1:3 internally are (5, -1).
Final Answer:
The coordinates of the point are (5, -1).
y=m1⋅y2+m2⋅y1m1+m2
- Let point A = (4, -3) which is (x1, y1)
- Let point B = (8, 5) which is (x2, y2)
- The ratio m1:m2 = 1:3, where m1 = 1 and m2 = 3.
- Using the formula for x:
x=m1⋅x2+m2⋅x1m1+m2
- Substitute the values:
x=1⋅8+3⋅41+3=8+124=204=5
- Using the formula for y:
y=m1⋅y2+m2⋅y1m1+m2
- Substitute the values:
y=1⋅5+3⋅(−3)1+3=5−94=−44=−1
- The coordinates of the point that divides the line segment in the ratio 1:3 internally are (5, -1).
The coordinates of the point are (5, -1).
Similar Questions
Find the coordinates of the point which divides the line segment joining the points (4, 3) and (8, 5)in the ratio 3 : 1 internally.
View SolutionFind the coordinates of the point which divides the line segment joining the points (4, -3) and (8,5) in the ratio 3:1 internally.
View SolutionFind the coordinates of the points which divides the line segment joining the points (6, 3) and (−4, 5) in the ratio 3 :2 internally.
View Solution(i) Find the coordinates of the point which divides the line segment joining the points (6;3) and (-4;5) in the ratio 3:2 internally
View SolutionFind the co-ordinates of the point which divides the line joining the points (2,-4,3) and (-4,5,-6) in the ratio 2:1
View SolutionFind the coordinates of the point which divides the line segment joining the points (1,−2,3) and (3,4,−5) in the ratio 2:3 (1) internally, and (2)externally
View Solution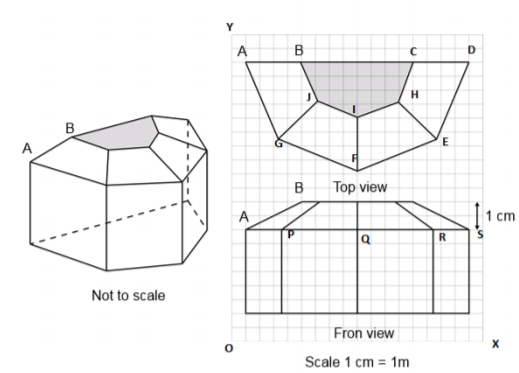
Refer to Front View Find the co-ordinates of the point which divides the line segment joining the points A and B in the ratio 1:3 internally. (i) (9.5,2.0) (ii) (2.0,9.5) (iii) (3.0,7.5) (iv) (2.0,8.5)
View SolutionFind the coordinates of the point which divides the line segment joining the points (1,2,3)and (3,4,5)in the ratio 2:3
(i) internally, and (ii) externally.
View SolutionFind the coordinates of the point which divides the line segments joining the points (6,3) and (−4,5) in the ratio 3:2 (i) internally and (ii) externally.
View SolutionFind the co-ordinates of a point which divides the line segment joining the points (5, 1) and (-10, 11) in the ratio 2 : 3 internally.
View Solution
