How many symmetry elements are there for a cubic structure or a crystal ?
To determine the total number of symmetry elements in a cubic structure or crystal, we can break down the analysis into systematic steps:
1. Identify the Types of Symmetry Elements:
- A cubic structure has several types of symmetry elements, including:
- Center of symmetry
- Axes of symmetry (different orders)
- Planes of symmetry
2. Count the Center of Symmetry:
- There is 1 center of symmetry in a cubic structure.
3. Count the Axes of Symmetry:
- Four-fold axes: There are 3 axes of four-fold symmetry (each axis passes through the center and the centers of opposite faces).
- Three-fold axes: There are 4 axes of three-fold symmetry (each axis passes through the vertices of the cube).
- Two-fold axes: There are 6 axes of two-fold symmetry (each axis passes through the midpoints of opposite edges).
4. Count the Planes of Symmetry:
- Rectangular planes: There are 3 rectangular planes of symmetry (each plane bisects the cube through the center and is parallel to a pair of opposite faces).
- Diagonal planes: There are 6 diagonal planes of symmetry (each plane bisects the cube diagonally, passing through opposite edges).
5. Total the Symmetry Elements:
- Now, we can sum all the symmetry elements counted:
- Center of symmetry: 1
- Four-fold axes: 3
- Three-fold axes: 4
- Two-fold axes: 6
- Rectangular planes: 3
- Diagonal planes: 6
Total = 1 (center) + 3 (four-fold) + 4 (three-fold) + 6 (two-fold) + 3 (rectangular) + 6 (diagonal) = 23 symmetry elements.
Final Answer:
The total number of symmetry elements in a cubic structure is 23.
- A cubic structure has several types of symmetry elements, including:
- Center of symmetry
- Axes of symmetry (different orders)
- Planes of symmetry
- There is 1 center of symmetry in a cubic structure.
- Four-fold axes: There are 3 axes of four-fold symmetry (each axis passes through the center and the centers of opposite faces).
- Three-fold axes: There are 4 axes of three-fold symmetry (each axis passes through the vertices of the cube).
- Two-fold axes: There are 6 axes of two-fold symmetry (each axis passes through the midpoints of opposite edges).
- Rectangular planes: There are 3 rectangular planes of symmetry (each plane bisects the cube through the center and is parallel to a pair of opposite faces).
- Diagonal planes: There are 6 diagonal planes of symmetry (each plane bisects the cube diagonally, passing through opposite edges).
- Now, we can sum all the symmetry elements counted:
- Center of symmetry: 1
- Four-fold axes: 3
- Three-fold axes: 4
- Two-fold axes: 6
- Rectangular planes: 3
- Diagonal planes: 6
The total number of symmetry elements in a cubic structure is 23.
Similar Questions
Knowledge Check
- Question 1 - Select One
A crystal is formed by two elements X and Y in cubic structure. X atoms are at the corners of a cube while Y atoms are at the face centre . The formula of the compound will be
AXYBXY2CX2Y3DXY3
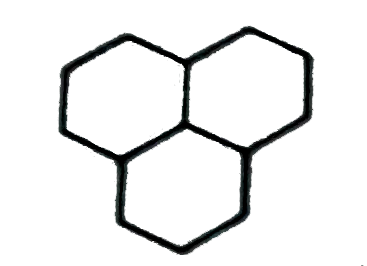
How many hydrogen atoms are present in the given structure ?View SolutionHow many elements can be there in the third period ?
View SolutionHow many transition series of elements are there in the periodic table.
View SolutionHow many unit cell are present in a cubic-shaped ideal crystal of NaCl of mass 1.0g?
View SolutionHow many unit cells are present in a cubic shaped ideal crystal of NaCl of mass 1.0 g ?
View SolutionHow many voids per point are present in cubic close packed structures of spheres ?
View SolutionHow many chiral carbons are present in following structure ?
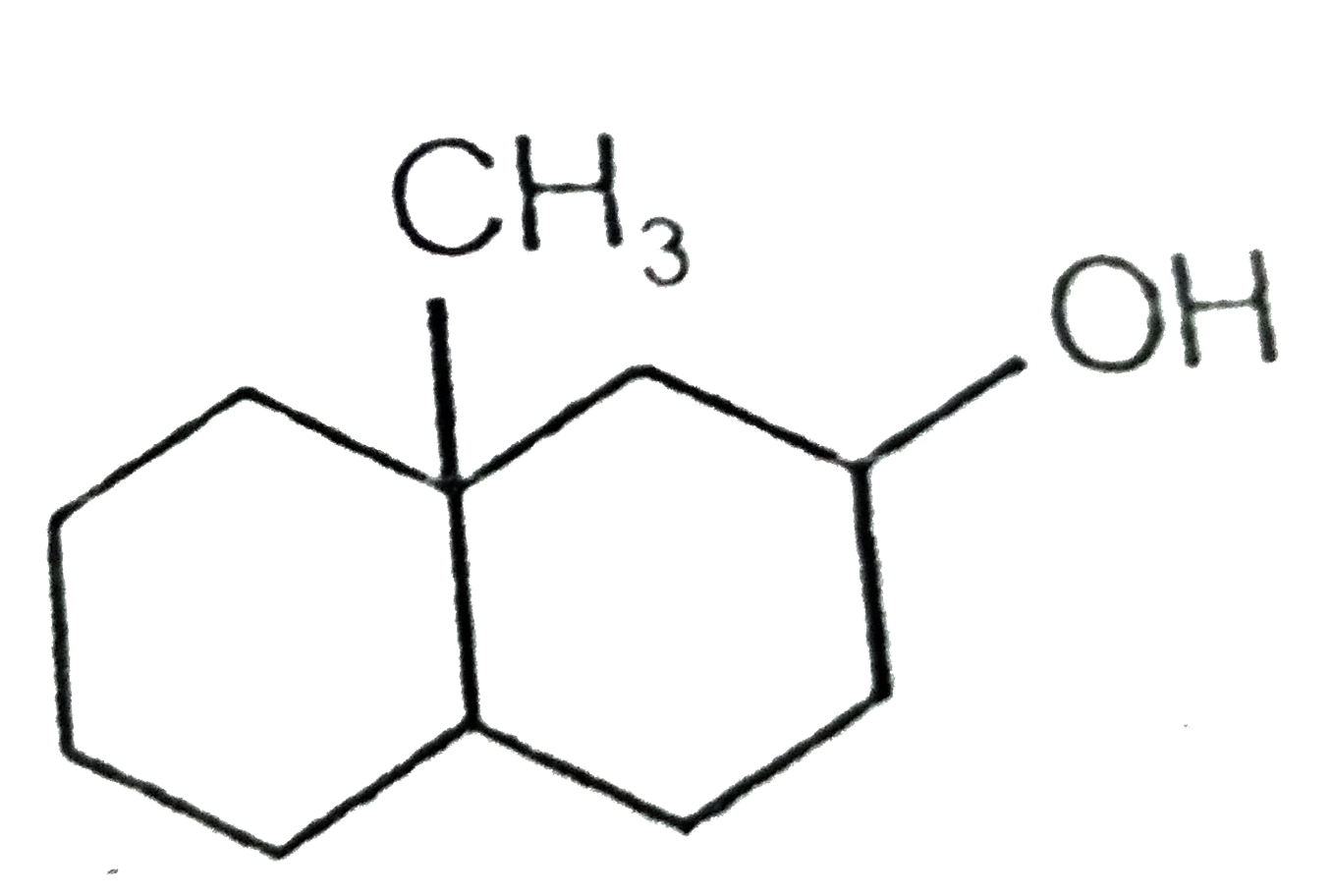 View Solution
View Solution

