Rahul Dravid wants to wear 6.023×1021 Ag atms in the form of a ring. His Silver Gold Copper alloy ring consists of 20% of Silver. The mass of the ring is 0.9 x. What is x?
The correct Answer is:6
To solve the problem step by step, let's break it down:
Step 1: Determine the number of moles of silver required
Rahul Dravid wants to wear 6.023×1021 Ag atoms. To find the number of moles of silver, we use Avogadro's number, which is 6.023×1023 atoms/mole.
Number of moles of silver=Number of atomsAvogadro's number=6.023×10216.023×1023=0.01 moles
Step 2: Calculate the total mass of silver in the ring
The ring is made of an alloy that contains 20% silver. The total mass of the ring is given as 0.9x. Therefore, the mass of silver in the ring can be calculated as:
Mass of silver=20% of total mass=0.2×(0.9x)=0.18x
Step 3: Calculate the number of moles of silver in the ring
The number of moles of silver can also be calculated using its mass and molar mass. The atomic mass of silver (Ag) is 108 g/mol. Therefore, the number of moles of silver in the ring is:
Number of moles of silver=Mass of silverMolar mass of silver=0.18x108
Step 4: Set up the equation
Since we know from Step 1 that the number of moles of silver required is 0.01 moles, we can set up the equation:
0.18x108=0.01
Step 5: Solve for x
Now we can solve for x:
0.18x=0.01×108
0.18x=1.08
x=1.080.18=6
Conclusion
The value of x is 6.
---
Rahul Dravid wants to wear 6.023×1021 Ag atoms. To find the number of moles of silver, we use Avogadro's number, which is 6.023×1023 atoms/mole.
The ring is made of an alloy that contains 20% silver. The total mass of the ring is given as 0.9x. Therefore, the mass of silver in the ring can be calculated as:
The number of moles of silver can also be calculated using its mass and molar mass. The atomic mass of silver (Ag) is 108 g/mol. Therefore, the number of moles of silver in the ring is:
Since we know from Step 1 that the number of moles of silver required is 0.01 moles, we can set up the equation:
Now we can solve for x:
0.18x=1.08
x=1.080.18=6
The value of x is 6.
Similar Questions
Rahul Dravid wants to wear 6.023×1021 Ag atms in the form of a ring. His Silver Gold Copper alloy ring consists of 20% of Silver. The mass of the ring is 0.9 x. What is x?
View SolutionA charge of 16×10−9C is fixed at the origin of coordinates. A second charge of unknow magnitude is at x=3m,y=0 and a third charge of 12×10−9C is at x=6m, y=0. What is the value of the unknown charge if the resultant field at x=8m, y=0 is 20.25 N/C directed towards positive x-axis ?
View SolutionFind the average time between collisions for electrons in the copper at 20∘C. The density of copper is 8.95gcm−3, molar mass of copper is 63.5gmol−1, Avogadro number is 6.02×1023 electrons per mol and resistivity of copper is 1.7×10−8Ωm
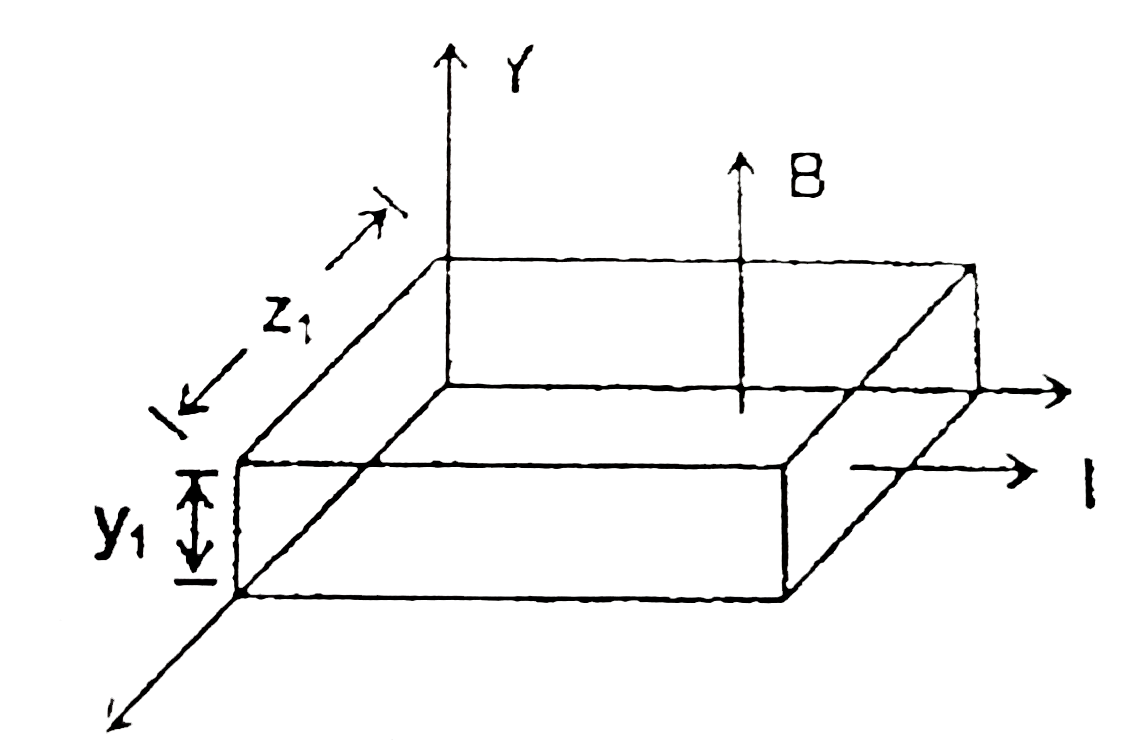
View SolutionThe basic principle underlying the Hall effect is the Lorentz force. When an electron moves along a direction perpendicular to an applied magnetic field, it experiences a force acting normal to both the directions and moves in response to this force and the force exerted by the internal electric field. For an n-type, bar-shaped semiconductor, the carriers are predominantly electrons of bulk density n. We assume that the constant current I flows along the x-axis from left to right in the presence of a magnetic field toward y-axis. Electrons subjected to the lorentz force initially drift away from the current line toward the negative z-axis, resulting in an excess surface electrical charge on the sides of the sample. This charge results in the hall voltage, a potential drop across the two sides of the sample.
The transverse voltage is the hall voltage VH and its magnitude is equal to IB/qnd, where I is the current, B is the magnetic field, d is the sample thickness and q is the elementary charge. A silver ribbon lies as shown in the adjacent figure. (z1=11.8mm and y1=0.23mm) carrying a current of 120A in the x-direction in a uniform magnetic field B=0.95T. If electron density is 5.85×1028/m3, then
What is the value of hall emf ?
View SolutionHow many Ag atoms are there in 0.001 g of silver? Take atomic mass of Ag = 108 and Avogadro's number =6.023×1023.
View SolutionA ring of radius R=4m is made of a highly dense material. Mass of the ring is m1=5.4×109kg distributed uniformly over its circumference. A highly dense particle of mass m2=6×108kg is placed on the axis of the ring at a distance x0=3m from the centre. Neglecting all other forces, except mutual gravitational interacting of the two. Caculate
(i) displacemental of the ring when particle is at the centre of ring, and
(ii) speed of the particle at that instant.
View SolutionHalf lives of two isotopes X and Y of a material are known to be 2×109 years and 4×109 years respectively if a planet was formed with equal number of these isotopes, then the current age of planet, given that currently the material has 20% of X and 80% of Y by number, will be:
View SolutionEinstein in 1905 proppunded the special theory of relativity and in 1915 proposed the general theory of relativity. The special theory deals with inertial frames of reference. The general theory of relativity deals with problems in which one frame of reference. He assumed that fixed frame is accelerated w.r.t. another frame of reference of reference cannot be located. Postulated of special theory of realtivity
● The laws of physics have the same form in all inertial systems.
● The velocity light in empty space is a unicersal constant the same for all observers.
● Einstein proved the following facts based on his theory of special relativity. Let v be the velocity of the speceship w.r.t a given frame of reference. The obserations are made by an observer in that reference frame.
● All clocks on the spaceship wil go slow by a factor √1−v2/c2
● All objects on the spaceship will have contracted in length by a factor √1−v2/c2
● The mass of the spaceship increases by a factor √1−v2/c2
● Mass and energy are interconvertable E=mc2
The speed of a meterial object can never exceed the velocity of light.
● If two objects A and B are moving with velocity u and v w.r.t each other along the x-axis, the relative velocity of A w.r.t. B=u−v1−uv/v2
The momentum of an electron moving with a speed 0.6c (Rest mass of electron is 9.1×10−31kg)
View SolutionAn iron ring measuring 15.00 cm in diameter is a be shrunk on a pulley which is 15.05 cm in diamer. All measurements refer to the room temperature 200C. To What minimum temperature should the ring be heated to make the job possible? Calculate the strain developed in the ring when in comes to the room temperature. Coefficient of linear expansion of iron =12×10−6^0C−1.
View SolutionAn iron ring measuring 15.00 cm in diameter is a be shrunk on a pulley which is 15.05 cm in diameter. All measurements refer to the room temperature 200C. To What minimum temperature should the ring be heated to make the job possible? Calculate the strain developed in the ring when in comes to the room temperature. Coefficient of linear expansion of iron =12×10−6C−1.
View Solution
