Rate of decomposition of a substance increases by a factor 2.25 for 1.5 times increase in conentration at constant temperature . Calculate the order of reaction.
The correct Answer is:2
To solve the problem of determining the order of reaction based on the given information, we can follow these steps:
Step 1: Understand the Rate Law
The rate of a reaction can be expressed by the rate law:
Rate=k(A)n
where:
- k is the rate constant,
- (A) is the concentration of the reactant,
- n is the order of the reaction.
Step 2: Set Up the Initial and New Conditions
According to the problem, the rate of decomposition increases by a factor of 2.25 when the concentration increases by a factor of 1.5.
Let:
- Initial concentration = (A)
- New concentration = 1.5(A)
- Initial rate = Rate1=k(A)n
- New rate = Rate2=k(1.5(A))n
Step 3: Write the Relationship Between Rates
From the information given, we can express the relationship between the new and initial rates:
Rate2Rate1=2.25
Substituting the expressions for the rates:
k(1.5(A))nk(A)n=2.25
This simplifies to:
(1.5)n1=2.25
Step 4: Solve for n
Now we need to solve the equation:
(1.5)n=2.25
We can express 2.25 as:
2.25=(1.5)2
Thus, we have:
(1.5)n=(1.5)2
Since the bases are the same, we can equate the exponents:
n=2
Conclusion
The order of the reaction is n=2.
The rate of a reaction can be expressed by the rate law:
Rate=k(A)n
where:
- k is the rate constant,
- (A) is the concentration of the reactant,
- n is the order of the reaction.
According to the problem, the rate of decomposition increases by a factor of 2.25 when the concentration increases by a factor of 1.5.
- Initial concentration = (A)
- New concentration = 1.5(A)
- Initial rate = Rate1=k(A)n
- New rate = Rate2=k(1.5(A))n
From the information given, we can express the relationship between the new and initial rates:
Rate2Rate1=2.25
Substituting the expressions for the rates:
k(1.5(A))nk(A)n=2.25
This simplifies to:
(1.5)n1=2.25
Now we need to solve the equation:
(1.5)n=2.25
We can express 2.25 as:
2.25=(1.5)2
Thus, we have:
(1.5)n=(1.5)2
Since the bases are the same, we can equate the exponents:
n=2
The order of the reaction is n=2.
Similar Questions
Knowledge Check
For a chemical reaction A→B, the rate of reaction increases by a factor of 1.837 when the concentration of A is increased by 1.5 time. The order of reaction with respect to A is:
A1B1.5C2D2.5
In a reaction A→B the rate of reaction increases two times on increasing the concentration of the reactant four times, then order of reaction is
View SolutionThe rate of reaction between A and B increases by a factor of 100, when the concentration with respect to A is increased 10 folds, the order of reaction w.r.t. A is
View SolutionRate of reaction increase with temperature :-
View SolutionFor the catalytic decomposition of a substance , half - lives are given below .
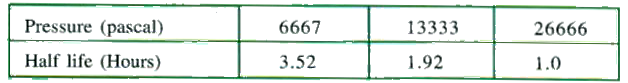
Calculate the order of reaction.
View SolutionRaiisng the concentration of a particular reactant by a factor of 5 increases the reaction rate 25 times. What is the kinetic order of this reactant?
View SolutionFor a reaction 3A→ Products, it is found that the rate of reaction doubles. If the concentration of A is increased four times, calculated the order of reaction.
View SolutionThe rate constant of a reaction increases linearly with increase in temperature.
View Solution
