Which statement(s) is correct,
for ideal gas is zero
All of these
The correct Answer is:D
To solve the question regarding which statements are correct, we will analyze each statement based on the principles of thermodynamics.
1. Understanding Enthalpy and Internal Energy:
- We start with the definitions:
- Change in enthalpy (ΔH) at constant pressure is given by:
ΔH=CpΔT
- Change in internal energy (ΔU) at constant volume is given by:
ΔU=CvΔT
2. Relating Cp and Cv:
- The relationship between the heat capacities for an ideal gas is:
Cp−Cv=R
- This shows that the difference between the heat capacities at constant pressure and constant volume equals the universal gas constant R.
3. Analyzing the First Statement:
- The first statement claims:
ΔHΔT at constant pressure−ΔUΔT at constant volume=Cp−Cv
- From our earlier relationship, we can conclude that this is correct because:
Cp−Cv=R
4. Analyzing the Second Statement:
- The second statement claims:
ΔHΔT at constant pressure−ΔUΔT at constant volume>0
- Since Cp−Cv=R and R>0 for an ideal gas, this statement is also correct.
5. Analyzing the Third Statement:
- The third statement claims that:
ΔHΔV at constant temperature=0
- For an ideal gas, we know that:
H=U+PV=U+RT
- Since internal energy U is a function of temperature only, at constant temperature, ΔU does not change with volume. Thus:
ΔHΔV=0+RΔTΔV=0
- Therefore, this statement is also correct.
6. Conclusion:
- Since all three statements are correct, the final conclusion is that the correct option is "All of the above."
- We start with the definitions:
- Change in enthalpy (ΔH) at constant pressure is given by:
ΔH=CpΔT
- Change in internal energy (ΔU) at constant volume is given by:
ΔU=CvΔT
- The relationship between the heat capacities for an ideal gas is:
Cp−Cv=R
- This shows that the difference between the heat capacities at constant pressure and constant volume equals the universal gas constant R.
- The first statement claims:
ΔHΔT at constant pressure−ΔUΔT at constant volume=Cp−Cv
- From our earlier relationship, we can conclude that this is correct because:
Cp−Cv=R
- The second statement claims:
ΔHΔT at constant pressure−ΔUΔT at constant volume>0
- Since Cp−Cv=R and R>0 for an ideal gas, this statement is also correct.
- The third statement claims that:
ΔHΔV at constant temperature=0
- For an ideal gas, we know that:
H=U+PV=U+RT
- Since internal energy U is a function of temperature only, at constant temperature, ΔU does not change with volume. Thus:
ΔHΔV=0+RΔTΔV=0
- Therefore, this statement is also correct.
- Since all three statements are correct, the final conclusion is that the correct option is "All of the above."
Similar Questions
Which statement(s) is/are correct?
View SolutionWhich statement(s) is/are correct
View Solution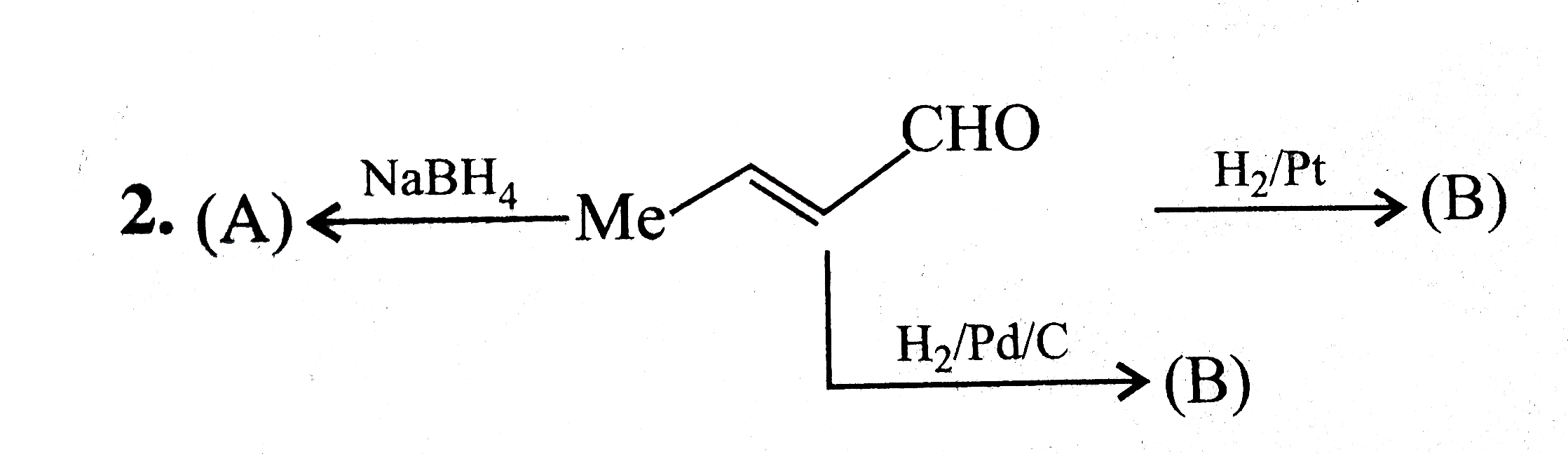
Which statement(s) is/are correct?
View SolutionWhich statement(s) is/are correct for the given reaction and compounds.

View SolutionCompound C4H8O2 exists in various strutures as shown:

Which statement(s) is/are correct?
View SolutionWhich statement (s) is /are correct ?
View SolutionWhich statement/s is/are correct?
View Solution
Among the following which statement(s) is/are correct:
View Solution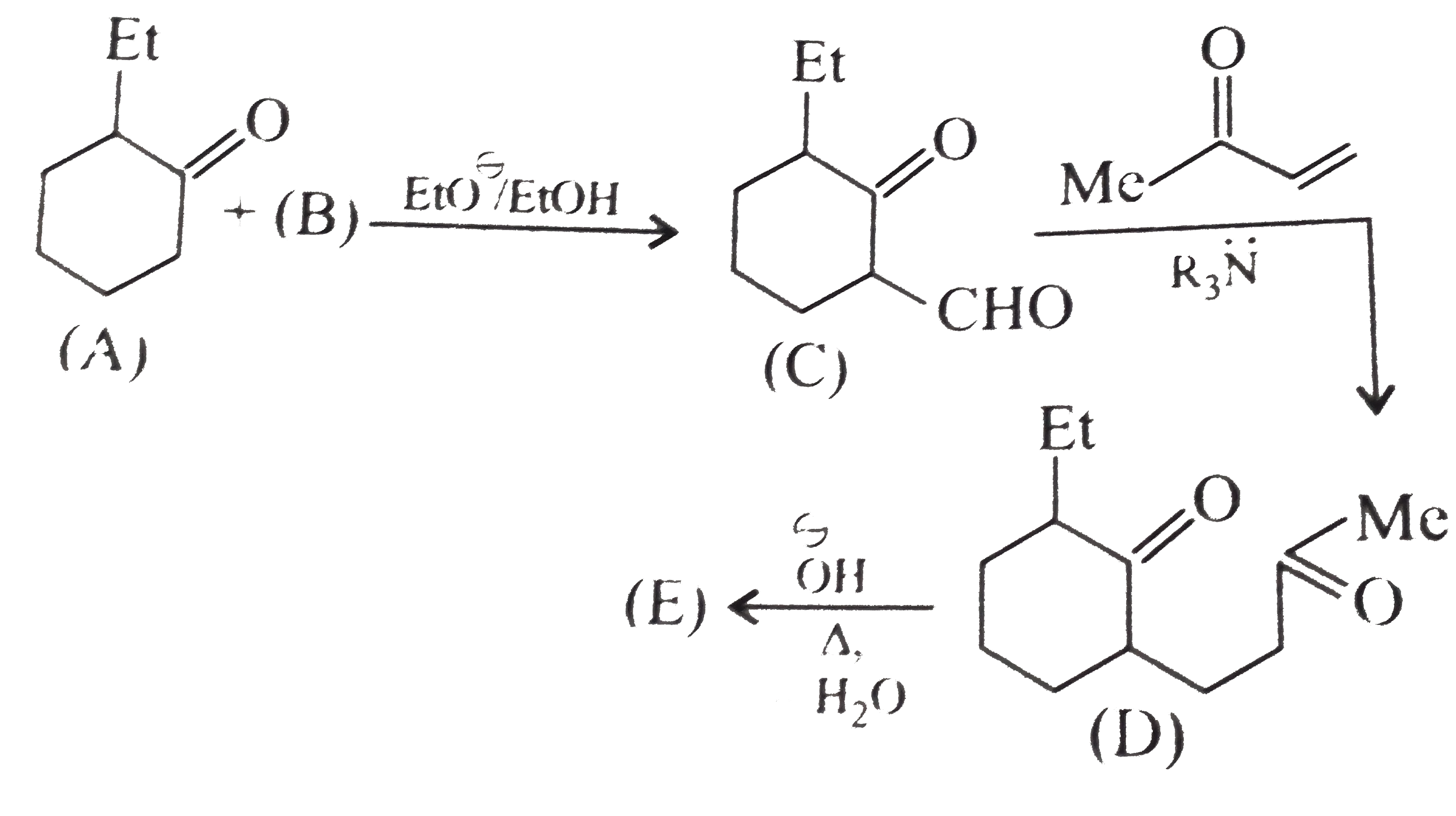
Which statement (s)is/are correct about the formation of (D) ?
View SolutionWhich statement (s) is/are correct about corrosion?
View Solution
