A sample of gas is compressed from an initial volume of 2v0 to v0 using three different processes.
First: Using reversible isothermal
Second: Using reversible adiabatic
Third: Using irreversible adiabatic under a constant external pressure then
Final temperature of gas will be highest at the end of third process.
Final temperature of gas will be highest at the end of second process
Enthalpy change of sample will be highest in isothermal process
Final pressure of gas will be highest at the end of second process.
The correct Answer is:A
To solve the problem of determining the work done during the compression of a gas from an initial volume of 2v0 to v0 using three different processes, we will analyze each process step by step.
Step 1: Understand the Processes
1. Reversible Isothermal Process: In this process, the temperature of the gas remains constant while it is compressed. The work done on the gas can be calculated using the formula:
Wisothermal=−nRTln(VfVi)
where Vf is the final volume, Vi is the initial volume, n is the number of moles, R is the universal gas constant, and T is the absolute temperature.
2. Reversible Adiabatic Process: In this process, there is no heat exchange with the surroundings. The work done can be calculated using the formula:
Wadiabatic=PiVi−PfVfγ−1
where γ is the heat capacity ratio (Cp/Cv), and Pi and Pf are the initial and final pressures.
3. Irreversible Adiabatic Process: In this process, the gas is compressed against a constant external pressure. The work done can be calculated as:
Wirreversible=−Pext(Vf−Vi)
where Pext is the constant external pressure.
Step 2: Calculate Work Done in Each Process
1. For Reversible Isothermal Process:
Wisothermal=−nRTln(v02v0)=nRTln(2)
2. For Reversible Adiabatic Process:
The work done in a reversible adiabatic process is generally less than that in an isothermal process for the same change in volume. The exact value depends on the specific heat capacities and the initial and final states of the gas.
3. For Irreversible Adiabatic Process:
The work done is given by:
Wirreversible=−Pext(v0−2v0)=Pext(v0)
Since Pext is less than the pressure in the reversible processes, the work done here will be the least.
Step 3: Compare the Work Done
From the analysis:
- Wisothermal>Wadiabatic>Wirreversible
Step 4: Determine Final Temperatures
- In the reversible isothermal process, the temperature remains constant.
- In the reversible adiabatic process, the temperature decreases as the gas is compressed.
- In the irreversible adiabatic process, the temperature also decreases but is generally lower than in the reversible adiabatic process due to the nature of irreversible processes.
Conclusion
The final temperatures after each process will be:
- Highest in the isothermal process.
- Intermediate in the reversible adiabatic process.
- Lowest in the irreversible adiabatic process.
Final Answer
The correct option is that the final temperature of the gas will be highest at the end of the isothermal process, followed by the reversible adiabatic, and lowest in the irreversible adiabatic process.
Wisothermal=−nRTln(VfVi)
where Vf is the final volume, Vi is the initial volume, n is the number of moles, R is the universal gas constant, and T is the absolute temperature.
Wadiabatic=PiVi−PfVfγ−1
where γ is the heat capacity ratio (Cp/Cv), and Pi and Pf are the initial and final pressures.
Wirreversible=−Pext(Vf−Vi)
where Pext is the constant external pressure.
Wisothermal=−nRTln(v02v0)=nRTln(2)
The work done in a reversible adiabatic process is generally less than that in an isothermal process for the same change in volume. The exact value depends on the specific heat capacities and the initial and final states of the gas.
The work done is given by:
Wirreversible=−Pext(v0−2v0)=Pext(v0)
Since Pext is less than the pressure in the reversible processes, the work done here will be the least.
- Wisothermal>Wadiabatic>Wirreversible
- In the reversible adiabatic process, the temperature decreases as the gas is compressed.
- In the irreversible adiabatic process, the temperature also decreases but is generally lower than in the reversible adiabatic process due to the nature of irreversible processes.
- Highest in the isothermal process.
- Intermediate in the reversible adiabatic process.
- Lowest in the irreversible adiabatic process.
The correct option is that the final temperature of the gas will be highest at the end of the isothermal process, followed by the reversible adiabatic, and lowest in the irreversible adiabatic process.
Similar Questions
A gas is expanded from volume V1 to V2 through three different process:
a. Reversible adiabatic
b. Reversible isothermal
c. Irreversible adiabatic (against a constant external pressure Pex)
The correct option isView SolutionA gaseous sample is generally allowed to do only expansion/compression type work against its surroundings The work done in case of an irreversible expansion ( in the intermediate stages of expansion/compression the states of gases are not defined). The work done can be calculated using
dw=−PextdV
while in case of reversible process the work done can be calculated using
dw=−PdV where P is pressure of gas at some intermediate stages. Like for an isothermal reversible process. Since P=nRTV, so
w=∫dW=−vf∫vinRTV.dV=−nRTln(VfVi)
Since dw=PdV so magnitude of work done can also be calculated by calculating the area under the PV curve of the reversible process in PV diagram.
If four identical samples of an ideal gas initially at similar state (P0,V0,T0) are allowed to expand to double their volumes by four different process.
I: by isothermal irreversible process
II: by reversible process having equation P2V= constant
III. by reversible adiabatic process
IV. by irreversible adiabatic expansion against constant external pressure.
Then, in the graph shown in the final state is represented by four different points then, the correct match can be
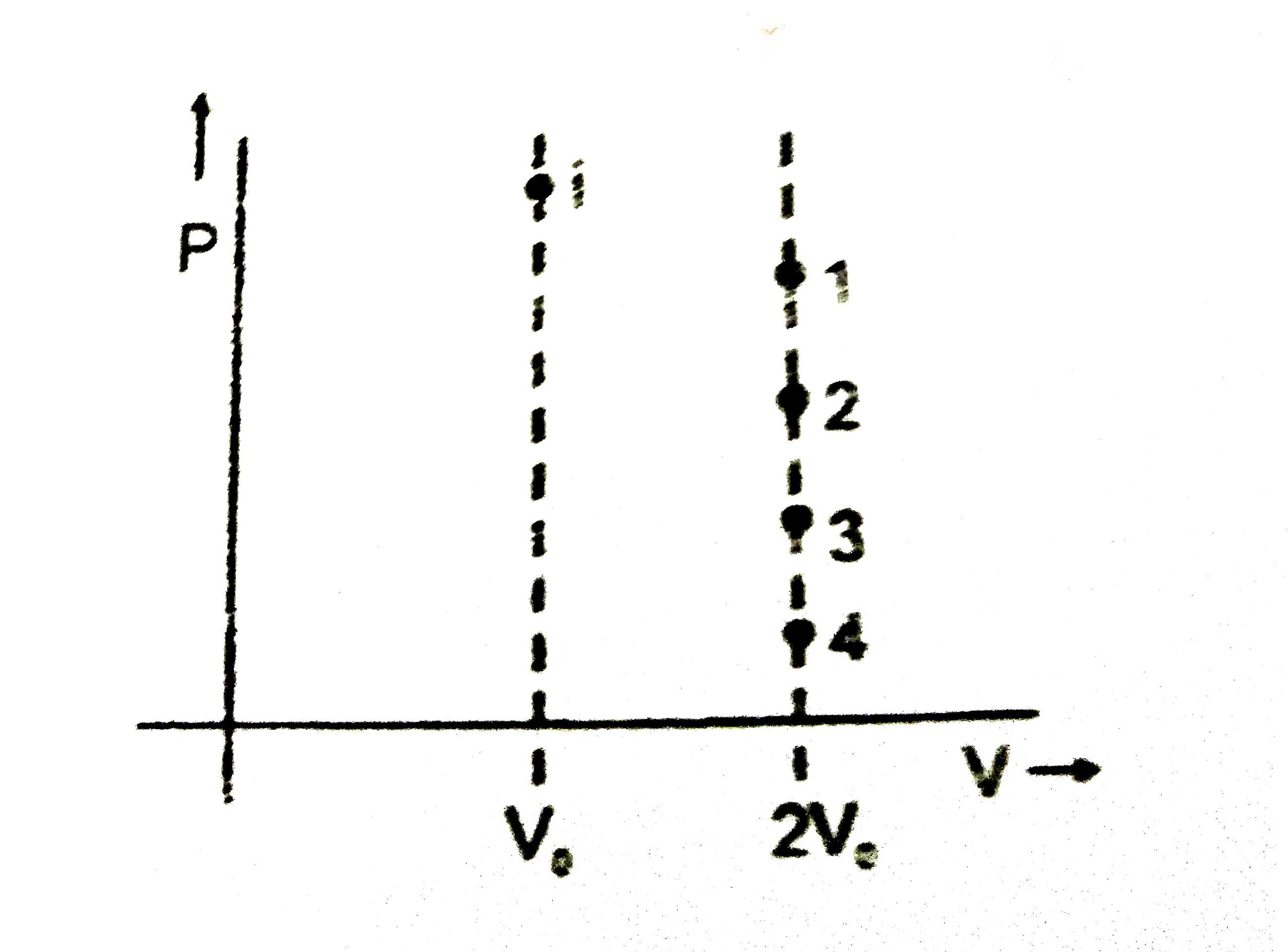 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A gas is expanded form volume V0→2V0 under three different processes as shown in the figure . Process 1 is isobaric process process 2 is isothermal and and process 3 is adiabatic .
Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes then
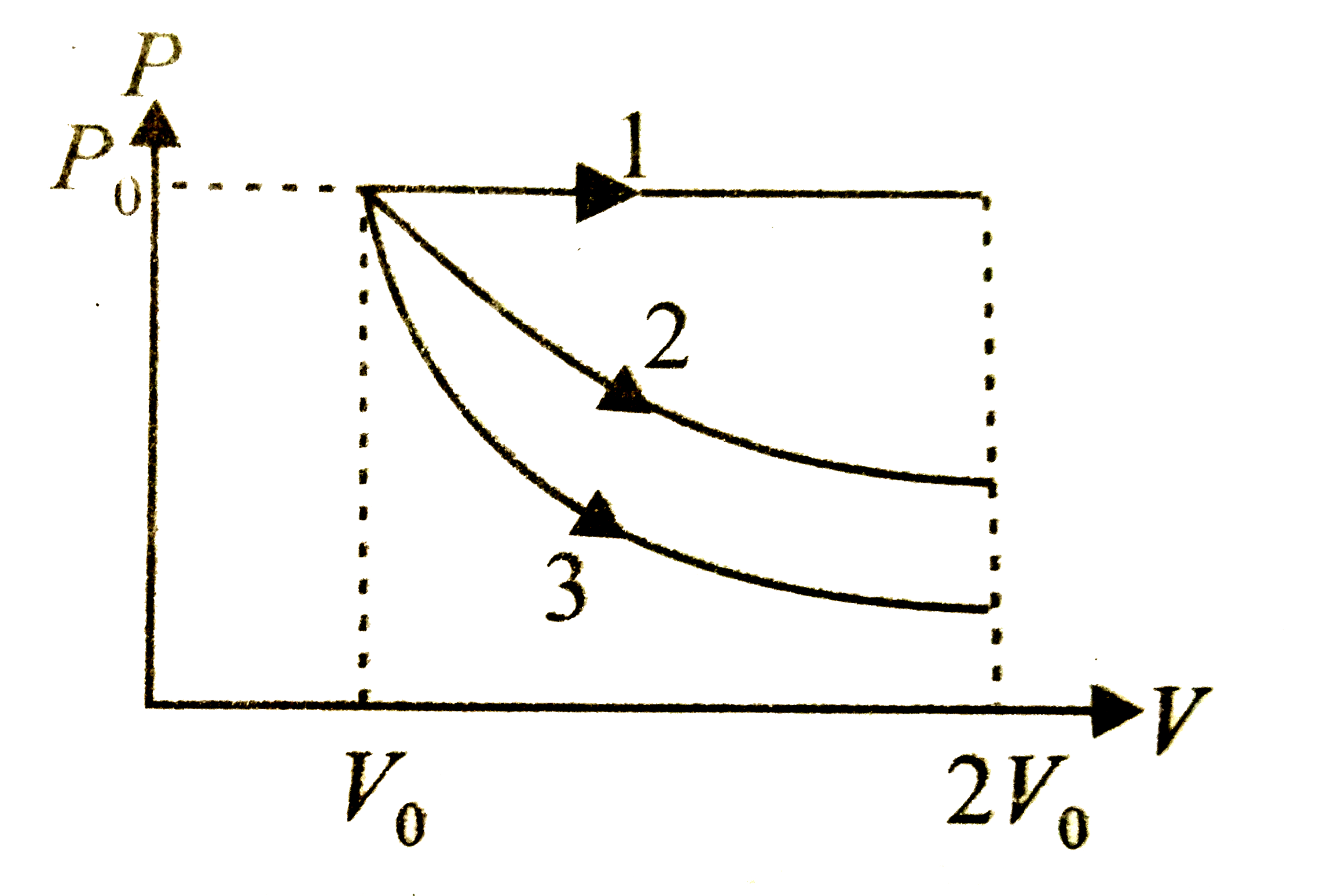 AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3
AΔU1>ΔU2>ΔU3BΔU1<ΔU2<ΔU3CΔU1<ΔU2<ΔU3DΔU1<ΔU2<ΔU3 - Question 2 - Select One
One mole of an ideal gas goes from an initial state A to final state B via two processs : It first undergoes isothermal expansion from volume V to 3V and then its volume is reduced from 3V to V at constant pressure. The correct P−V diagram representing the two process in (figure)
A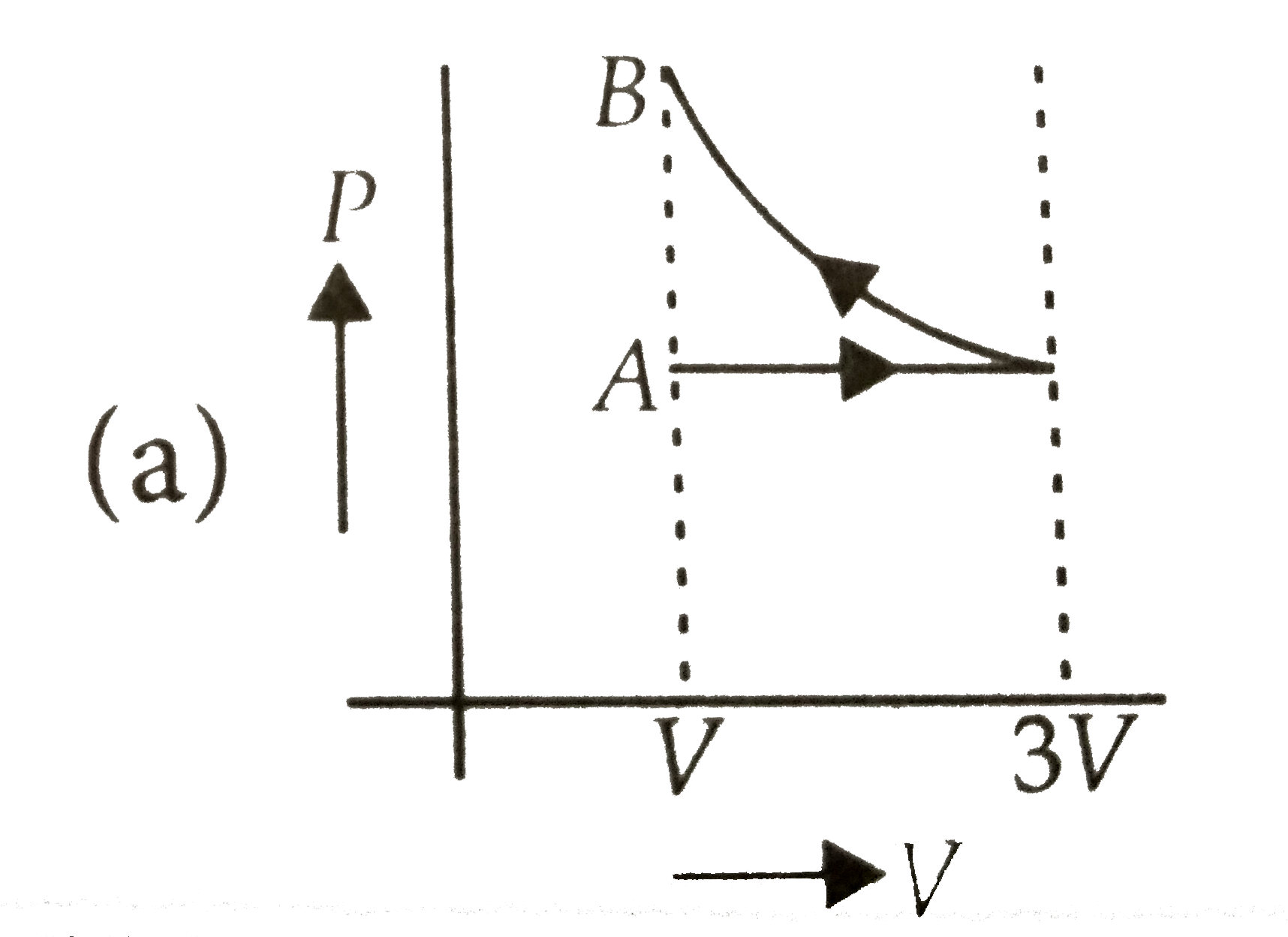 B
B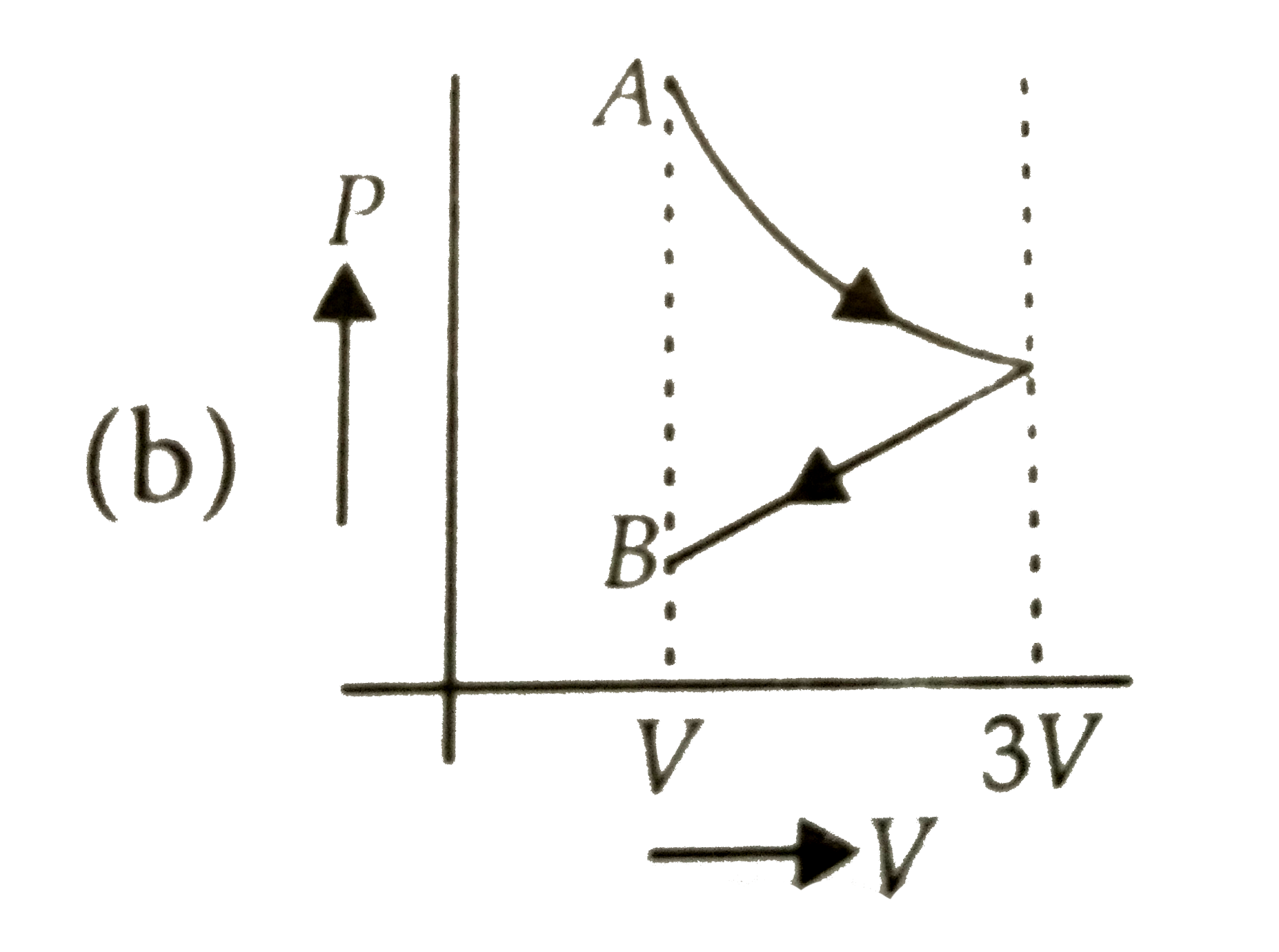 C
C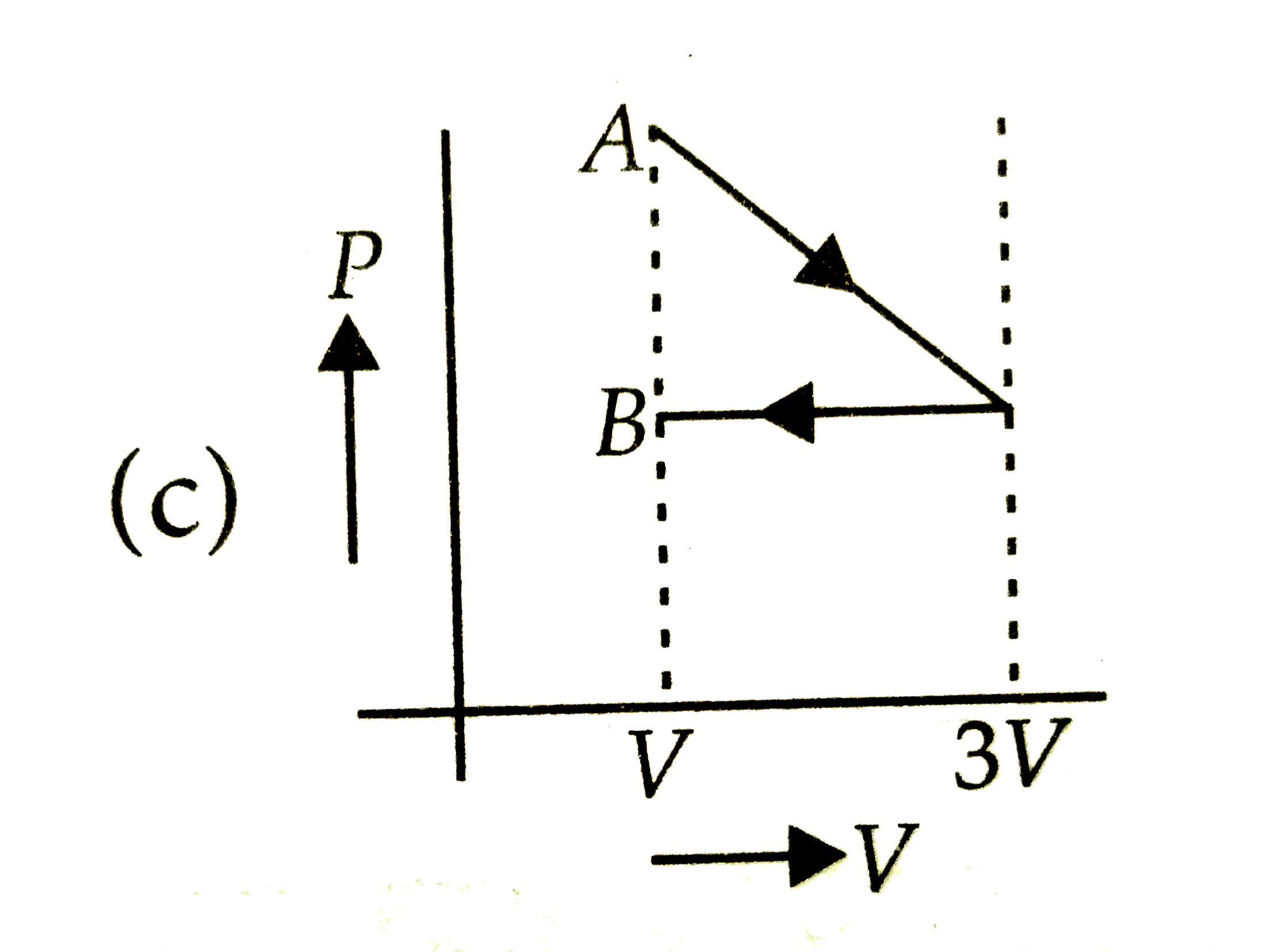 D
D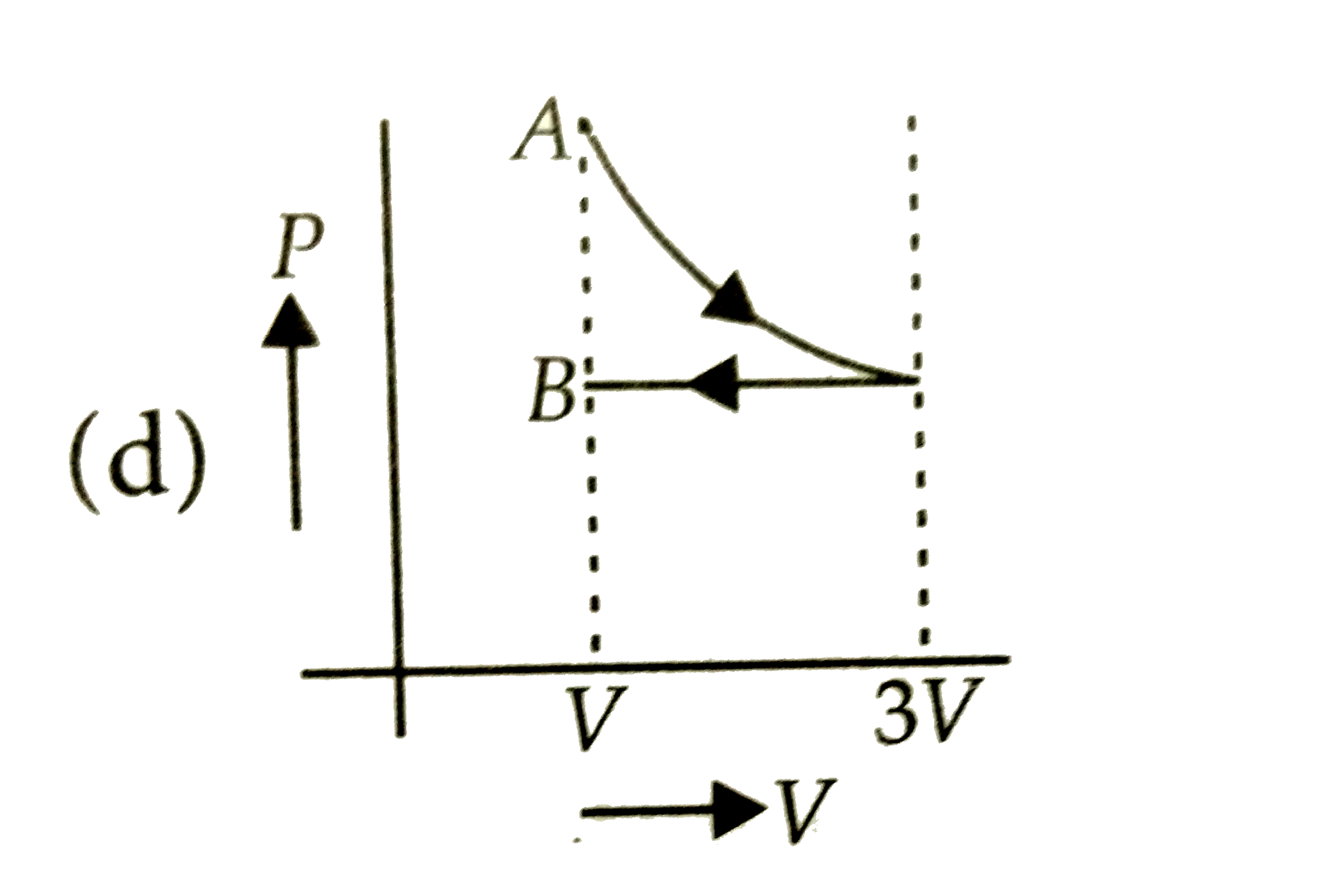
A gas is expanded from volume V0=2V0 under three different processes. Process 1 is isobaric process, process 2 is isothermal and process 3 is adiabatic. Let ΔU1,ΔU2andΔU3 be the change in internal energy of the gas in these three processes. then
 View Solution
View SolutionThere are two statement of same gas initially under similar initial state. Gases of both the samples are expanded. I s t sample using reversible isothermal process and I I n d sample using reversible adiabatic process till final pressure of both the samples becomes half of initial pressure. Then:
View SolutionThere are two statement of same gas initially under similar initial state. Gases of both the samples are expanded. Ist sample using reversible isothermal process and IInd sample using reversible adiabatic process till final pressure of both the samples becomes half of initial pressure. Then:
View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different paths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Order of magnitude of work is :View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Work done (in bar-L) on the gas in reversible isothermal compression is :View SolutionIf the boundary of system moves by an infinitesimal amount, the work involved is given by dw=−PextdV
for irreversible process w=−PextΔV (where ΔV=Vf−Vi)
for reversible process Pext=Pint±dP≅Pint
so for reversible isothermal process w=−nRTln.VfVi
2mole of an ideal gas undergoes isothermal compression along three different plaths :
(i) reversible compression from Pi=2 bar and Vi=8L to Pf=20 bar
(ii) a single stage compression against a constant external pressure of 20 bar, and
(iii) a two stage compression consisting initially of compression against a constant external pressure of 10 bar until Pgas=Pext, followed by compression against a constant pressure of 20 bar until Pgas=Pext
Work done on the gas in single stage compression is :View Solution

