An acidic indicator ionises as InH⇔In−+H+ . The molecular and ions of the indicator show different colours. The indicator changed it colour if its acidic of basic form completely predominant.
Dissociation constant of an acidic indicator is 10−5 . At what pH 80% of the indicator exists in molecular form ?
4.4
6.6
5.5
3.3
The correct Answer is:A
To find the pH at which 80% of the indicator exists in its molecular form, we can follow these steps:
Step 1: Understand the Dissociation of the Indicator
The dissociation of the acidic indicator can be represented as:
HIn⇌In−+H+
Step 2: Define the Dissociation Constant (Ka)
The dissociation constant Ka for the indicator is given as:
Ka=10−5
Step 3: Calculate pKa
To find pKa, we can use the formula:
pKa=−log(Ka)
Substituting the value of Ka:
pKa=−log(10−5)=5
Step 4: Determine the Ratio of Ionized to Unionized Forms
We know that 80% of the indicator exists in the molecular form (HIn) and 20% in the ionized form (In^-). This gives us the ratio:
(In−)(HIn)=2080=14
Step 5: Use the Henderson-Hasselbalch Equation
The Henderson-Hasselbalch equation relates the pH, pKa, and the ratio of the concentrations of the ionized and unionized forms:
pH=pKa+log((In−)(HIn))
Substituting the values we have:
pH=5+log(14)
Step 6: Calculate the Logarithm
We know that:
log(14)=log(1)−log(4)=0−0.602=−0.602
Thus:
pH=5−0.602=4.398
Step 7: Round the pH Value
Rounding the pH value gives:
pH≈4.4
Final Answer
The pH at which 80% of the indicator exists in molecular form is approximately 4.4.
---
The dissociation of the acidic indicator can be represented as:
HIn⇌In−+H+
The dissociation constant Ka for the indicator is given as:
Ka=10−5
To find pKa, we can use the formula:
pKa=−log(Ka)
Substituting the value of Ka:
pKa=−log(10−5)=5
We know that 80% of the indicator exists in the molecular form (HIn) and 20% in the ionized form (In^-). This gives us the ratio:
(In−)(HIn)=2080=14
The Henderson-Hasselbalch equation relates the pH, pKa, and the ratio of the concentrations of the ionized and unionized forms:
pH=pKa+log((In−)(HIn))
Substituting the values we have:
pH=5+log(14)
We know that:
log(14)=log(1)−log(4)=0−0.602=−0.602
Thus:
pH=5−0.602=4.398
Rounding the pH value gives:
pH≈4.4
The pH at which 80% of the indicator exists in molecular form is approximately 4.4.
Similar Questions
An acidic indicator ionises as InH⇔In−+H+ . The molecular and ions of the indicator show different colours. The indicator changed it colour if its acidic of basic form completely predominant.
An indicator with PK∈ = 5 is added to a solution with pH = 5 . What is the percentage of acidic form of the indicator
View SolutionAn acid indicator is represented by Hln.(Ka=10−5). The range of change of colour for the indicator is
View Solution
Knowledge Check
Which of the indicated H in the following is most acidic?
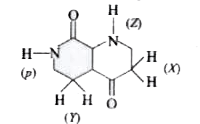 AXBYCZDp
AXBYCZDp
An acidic buffer contains equal concentrations of acid and salt. The dissociation constant of acid is 10−5. The PHof the buffer solution is
View SolutionAn acid-base indicator has a Ka=3.0×10−5. The acid form of the indicator is red and the basic form is blue. Then
View SolutionIf an acidic indicator HIn ionies as HIn⇔H++In−. To which maximum pH value its solution has distinct colour characterstic of HIn
View SolutionAn acid-base indicator has Ka=3.0×10−5. The acid form of the indicator is red and the basic form is blue. Then:
View SolutionWhat fraction of an indicator Hin is the basic form at a pH of 5 if the pKa of the indicator is 6?
View SolutionAn acid-base indicator has Ka=10−5. The acid form of the indicator is red and basic form is blue. Which of the following is//are correct?
View SolutionWhat fraction of an indicator Hin is in the basic form at a pH of 6 if pKa of the indicator is 5?
View Solution
