Using dimensional methods, verify the correctness of the following relations,
(i) a=v2/r,(ii)F=mrω2,(iii)S.T.= rhdg/2
In the above formulae 'r' stands for radius, 'm' for mass , 'ω' for angular velocity , 'v' for linear velocity , 'h' for height , 'd' for density and S.T. for surface tension.
To verify the correctness of the given relations using dimensional analysis, we will analyze each equation step by step.
(i) a=v2r
1. Identify the dimensions of each variable:
- Acceleration a: The dimensional formula is (a)=LT−2.
- Linear velocity v: The dimensional formula is (v)=LT−1.
- Radius r: The dimensional formula is (r)=L.
2. Calculate the dimensions of v2r:
- First, find the dimensions of v2:
(v2)=(v)×(v)=(LT−1)×(LT−1)=L2T−2
- Now, divide by the dimensions of r:
(v2)(r)=L2T−2L=LT−2
3. Compare the dimensions:
- The dimension of a is LT−2, which matches the dimension of v2r.
- Therefore, the equation a=v2r is correct.
(ii) F=mrω2
1. Identify the dimensions of each variable:
- Force F: The dimensional formula is (F)=MLT−2.
- Mass m: The dimensional formula is (m)=M.
- Radius r: The dimensional formula is (r)=L.
- Angular velocity ω: The dimensional formula is (ω)=T−1.
2. Calculate the dimensions of mrω2:
- First, find the dimensions of ω2:
(ω2)=(T−1)2=T−2
- Now, calculate the dimensions of mrω2:
(mrω2)=(m)×(r)×(ω2)=M×L×T−2=MLT−2
3. Compare the dimensions:
- The dimension of F is MLT−2, which matches the dimension of mrω2.
- Therefore, the equation F=mrω2 is correct.
(iii) S.T.=rhdg2
1. Identify the dimensions of each variable:
- Surface tension S.T.: The dimensional formula is (S.T.)=MLT−2.
- Radius r: The dimensional formula is (r)=L.
- Height h: The dimensional formula is (h)=L.
- Density d: The dimensional formula is (d)=ML−3.
- Gravitational acceleration g: The dimensional formula is (g)=LT−2.
2. Calculate the dimensions of rhdg:
- Now, calculate the dimensions of rhdg:
(rhdg)=(r)×(h)×(d)×(g)=L×L×(ML−3)×(LT−2)
- Simplifying this:
=L2×M×L−3×LT−2=ML−1T−2
3. Divide by 2:
- The division by 2 does not affect the dimensions, so:
(rhdg)2=ML−1T−2
4. Compare the dimensions:
- The dimension of S.T. is MLT−2, which does not match ML−1T−2.
- Therefore, the equation S.T.=rhdg2 is incorrect.
Summary of Results:
1. a=v2r is correct.
2. F=mrω2 is correct.
3. S.T.=rhdg2 is incorrect.
- Acceleration a: The dimensional formula is (a)=LT−2.
- Linear velocity v: The dimensional formula is (v)=LT−1.
- Radius r: The dimensional formula is (r)=L.
- First, find the dimensions of v2:
(v2)=(v)×(v)=(LT−1)×(LT−1)=L2T−2
- Now, divide by the dimensions of r:
(v2)(r)=L2T−2L=LT−2
- The dimension of a is LT−2, which matches the dimension of v2r.
- Therefore, the equation a=v2r is correct.
- Force F: The dimensional formula is (F)=MLT−2.
- Mass m: The dimensional formula is (m)=M.
- Radius r: The dimensional formula is (r)=L.
- Angular velocity ω: The dimensional formula is (ω)=T−1.
- First, find the dimensions of ω2:
(ω2)=(T−1)2=T−2
- Now, calculate the dimensions of mrω2:
(mrω2)=(m)×(r)×(ω2)=M×L×T−2=MLT−2
- The dimension of F is MLT−2, which matches the dimension of mrω2.
- Therefore, the equation F=mrω2 is correct.
- Surface tension S.T.: The dimensional formula is (S.T.)=MLT−2.
- Radius r: The dimensional formula is (r)=L.
- Height h: The dimensional formula is (h)=L.
- Density d: The dimensional formula is (d)=ML−3.
- Gravitational acceleration g: The dimensional formula is (g)=LT−2.
- Now, calculate the dimensions of rhdg:
(rhdg)=(r)×(h)×(d)×(g)=L×L×(ML−3)×(LT−2)
- Simplifying this:
=L2×M×L−3×LT−2=ML−1T−2
- The division by 2 does not affect the dimensions, so:
(rhdg)2=ML−1T−2
- The dimension of S.T. is MLT−2, which does not match ML−1T−2.
- Therefore, the equation S.T.=rhdg2 is incorrect.
1. a=v2r is correct.
2. F=mrω2 is correct.
3. S.T.=rhdg2 is incorrect.
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - VERY SHORT ANSWER TYPE QUESTIONS
24 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - NUMERICAL EXERCISE (LEVEL-1)
17 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
Similar Questions
Knowledge Check
A stone of mass M tied at the end of a string, is moving in a circular of radius R, with a constant angular velocity ω. The work done on the stone, in any half circle I s
AπMR2ω2B2MR2ω2CMR2ω2Dzero
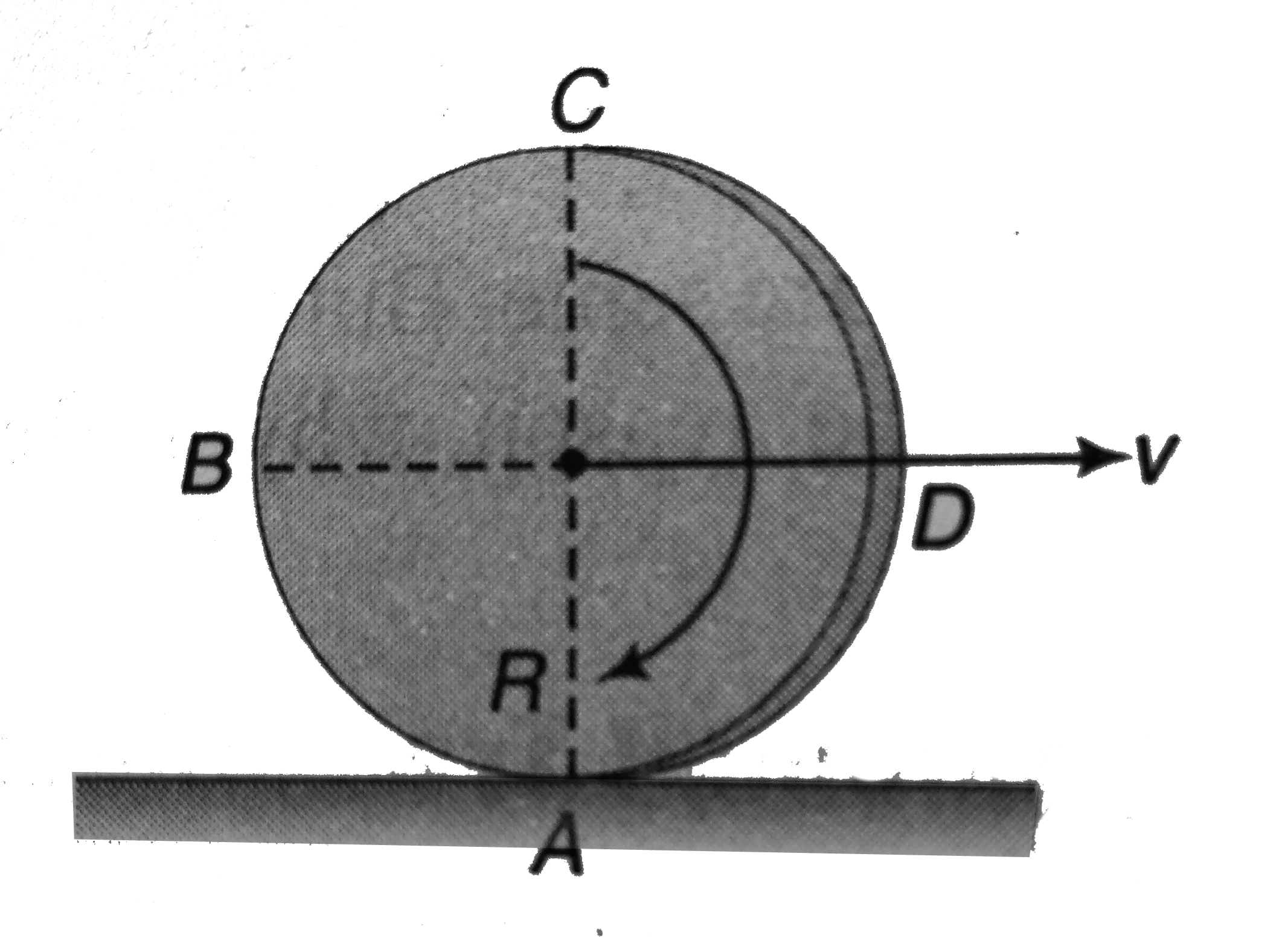
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionThe rotaitonal kinetic energy E=12Iω2. Use this equation to get the dimensional formula for ω, where I is the moment of inertia and ω is the angular velocity.
View SolutionDifferentiate the following w.r.t. x or t or u as the case may be:
s=t2(t+1)−1
View Solution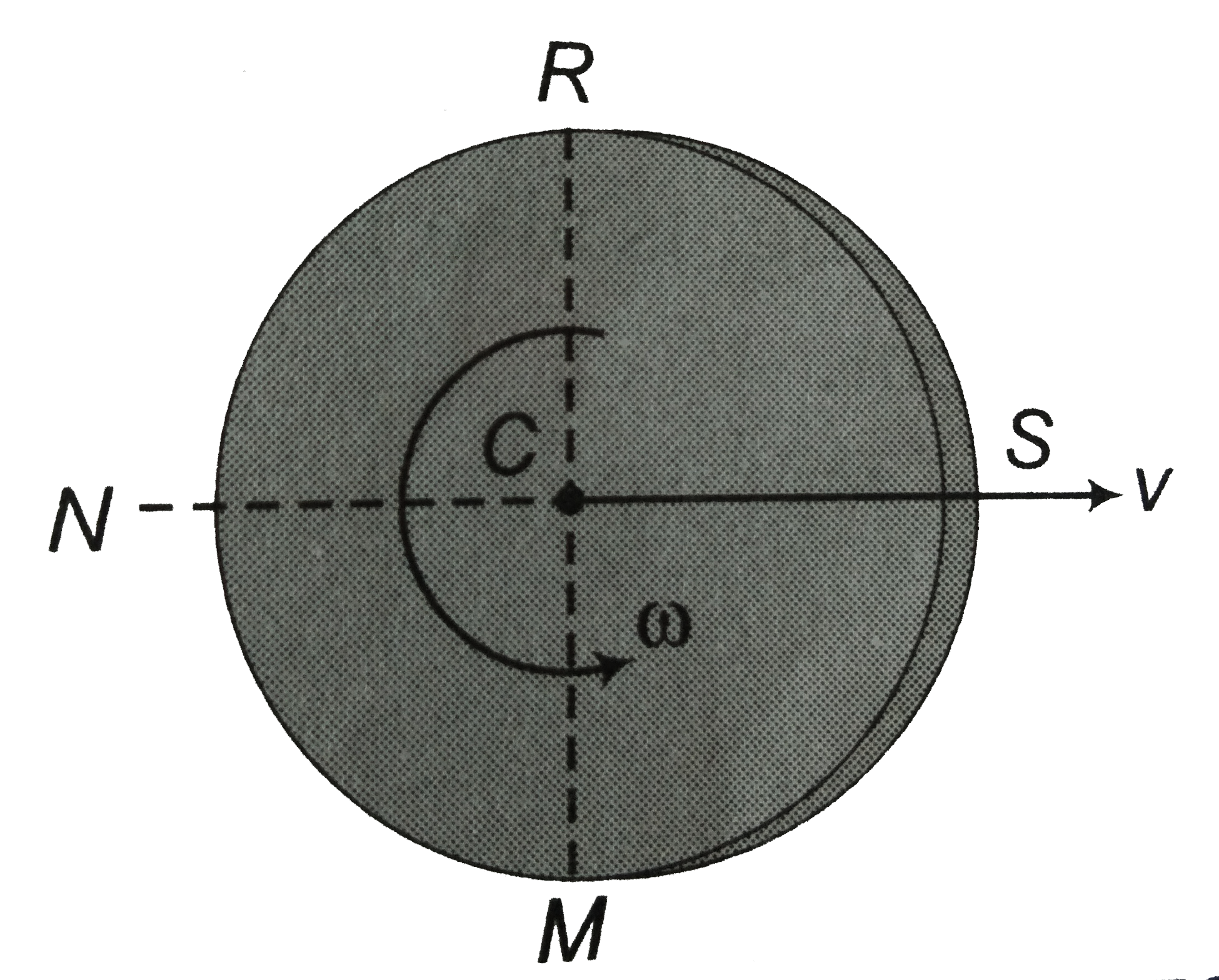
In the figure shown omega = v/2R in terms of i and j find the linear velocities of particles M,N,R and S .
View SolutionA disc has mass 'M" and radius 'R'. How much tangential force should be applied to the rim of the disc so as to rotate with angular velocity ω in time 't'?
View SolutionA disc of radius R is moving on a rough horizontal surface with velocity v and angular speed ω at an instant as shown in figure. Choose the correct statement.

View Solution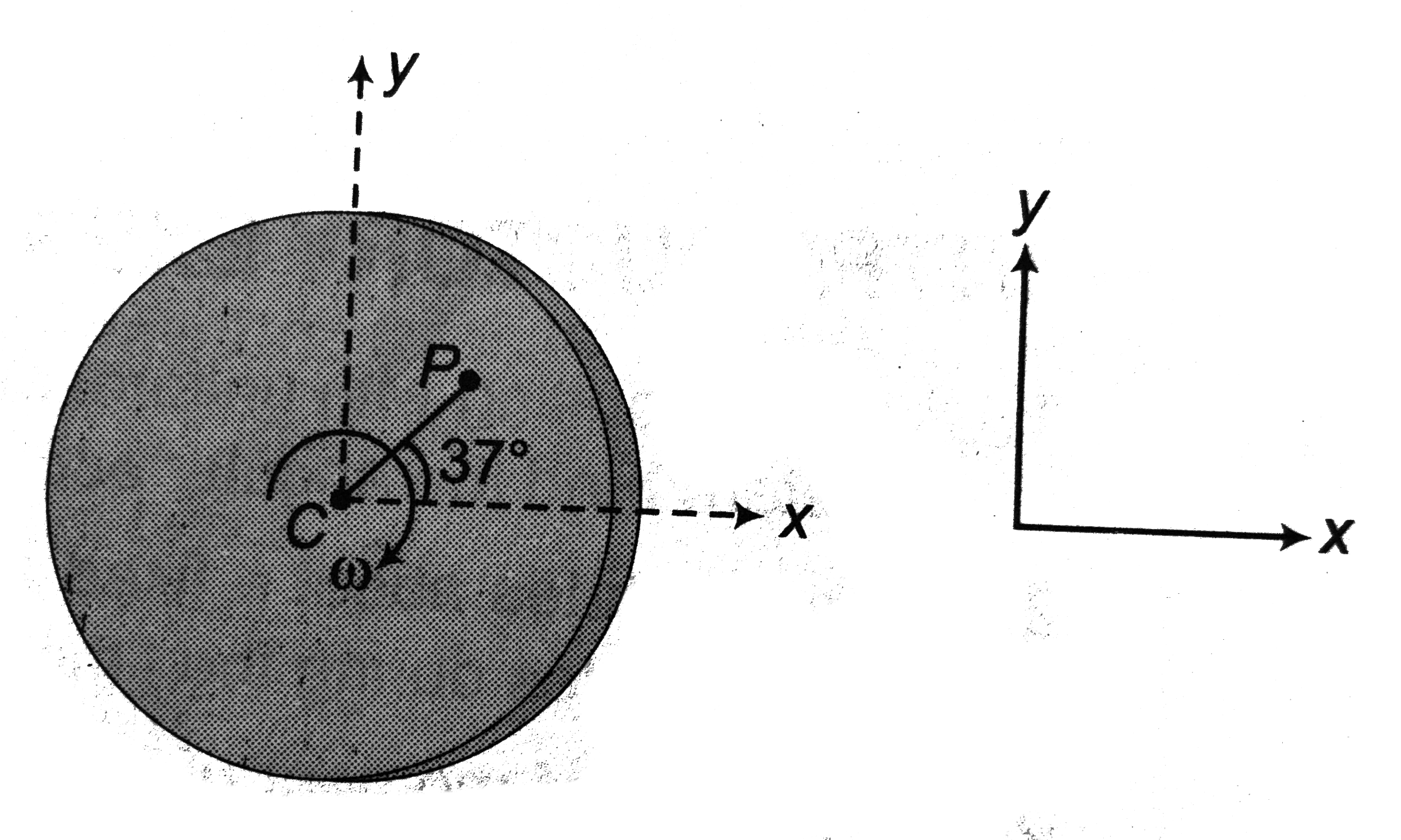
A circular disc is rotating with an angular speed (in radian per sec)
ω=2t2
given, CP=2m
In terms of ˆi,ˆj and ˆk at t=1s
find,
(a). ω
(b). α
(c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying P
View Solution
