Out of the following the correct order of dimensions of mass increases is
(A) Velocity (B) Power
(C ) Graviational Constant
A, B , C
C, A, B
A, C, B
B, C, A
The correct Answer is:B
To determine the correct order of dimensions of mass increases for the given quantities (Velocity, Power, and Gravitational Constant), we will analyze the dimensions of each quantity step by step.
Step 1: Determine the dimension of Velocity
- Velocity is defined as displacement per unit time.
- The dimension of displacement (length) is denoted as L and time is denoted as T.
- Therefore, the dimension of velocity is:
(Velocity)=LT=LT−1
Step 2: Determine the dimension of Power
- Power is defined as work done per unit time.
- The dimension of work is given by force times distance. The dimension of force is MLT−2 (from Newton's second law), and distance has the dimension L.
- Thus, the dimension of work is:
(Work)=(Force)×(Distance)=(MLT−2)×L=ML2T−2
- Now, since power is work done per unit time, we have:
(Power)=(Work)(Time)=ML2T−2T=ML2T−3
Step 3: Determine the dimension of Gravitational Constant
- The gravitational constant G can be derived from Newton's law of gravitation, which states that the gravitational force F between two masses m1 and m2 separated by a distance r is given by:
F=Gm1m2r2
- Rearranging this gives:
G=Fr2m1m2
- The dimension of force F is MLT−2, and the dimension of r2 is L2. The masses m1 and m2 both have the dimension M.
- Therefore, the dimension of G is:
(G)=MLT−2⋅L2M2=M−1L3T−2
Step 4: Compare the dimensions
Now we have the dimensions for each quantity:
- Velocity: (V)=LT−1 (mass dimension = M0)
- Power: (P)=ML2T−3 (mass dimension = M1)
- Gravitational Constant: (G)=M−1L3T−2 (mass dimension = M−1)
Step 5: Order the dimensions of mass
Now we can order them based on the dimension of mass:
1. Gravitational Constant G has the lowest mass dimension (M−1).
2. Velocity V has a mass dimension of M0.
3. Power P has the highest mass dimension (M1).
Thus, the correct order of the dimensions of mass increases is:
G<V<P
Final Answer
The correct order of dimensions of mass increases is:
(C) Gravitational Constant < (A) Velocity < (B) Power
---
- Velocity is defined as displacement per unit time.
- The dimension of displacement (length) is denoted as L and time is denoted as T.
- Therefore, the dimension of velocity is:
(Velocity)=LT=LT−1
- Power is defined as work done per unit time.
- The dimension of work is given by force times distance. The dimension of force is MLT−2 (from Newton's second law), and distance has the dimension L.
- Thus, the dimension of work is:
(Work)=(Force)×(Distance)=(MLT−2)×L=ML2T−2
- Now, since power is work done per unit time, we have:
(Power)=(Work)(Time)=ML2T−2T=ML2T−3
- The gravitational constant G can be derived from Newton's law of gravitation, which states that the gravitational force F between two masses m1 and m2 separated by a distance r is given by:
F=Gm1m2r2
- Rearranging this gives:
G=Fr2m1m2
- The dimension of force F is MLT−2, and the dimension of r2 is L2. The masses m1 and m2 both have the dimension M.
- Therefore, the dimension of G is:
(G)=MLT−2⋅L2M2=M−1L3T−2
Now we have the dimensions for each quantity:
- Velocity: (V)=LT−1 (mass dimension = M0)
- Power: (P)=ML2T−3 (mass dimension = M1)
- Gravitational Constant: (G)=M−1L3T−2 (mass dimension = M−1)
Now we can order them based on the dimension of mass:
1. Gravitational Constant G has the lowest mass dimension (M−1).
2. Velocity V has a mass dimension of M0.
3. Power P has the highest mass dimension (M1).
G<V<P
The correct order of dimensions of mass increases is:
(C) Gravitational Constant < (A) Velocity < (B) Power
Topper's Solved these Questions
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - EXERCISE - II
61 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- UNITS AND MEASUREMENTBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTEXERCISE - PRACTICE EXERCISE
45 Videos
- SEMICONDUCTOR DEVICESBOOK - AAKASH SERIESCHAPTER - SEMICONDUCTOR DEVICESEXERCISE - EXERCISE - III
3 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH SERIESCHAPTER - UNITS AND MEASUREMENTSEXERCISE - EXERCISE -3
66 Videos
Similar Questions
Knowledge Check
Find out correct orders :
A B
B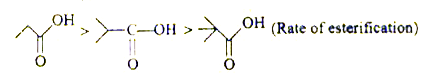 C
C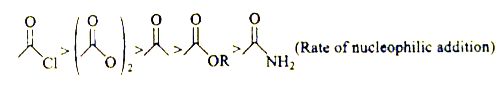 D
D
Mark out the correct increasing order of radius.
AAs3−<Br−<K+<Mg2+BMg2+<K+<Br−<As3−CMg2+<K+<As3−<Br−DK+<Mg2+<Br−<As3−
Which of the following is the correct order for increasing bond angle ?
View SolutionThe correct order of increasing order of size is
View SolutionThe correct order of increasing radii are
View SolutionThe correct order of reducing power off MH3 is:
View SolutionArrange the following in increasing order of dielectric constant :
View SolutionWhich of the following gives the correct increasing order of acid strength?
View Solution
