The minimum number of non coplanar forces that can keep a particle in equilibrium is
1
2
3
4
The correct Answer is:D
To determine the minimum number of non-coplanar forces required to keep a particle in equilibrium, we can follow these steps:
Step 1: Understand the concept of equilibrium
A particle is said to be in equilibrium when the net force acting on it is zero. This means that the vector sum of all forces acting on the particle must cancel each other out.
Hint: Remember that equilibrium requires the net force to be zero.
Step 2: Define non-coplanar forces
Non-coplanar forces are forces that do not lie in the same plane. This means that these forces act in three-dimensional space.
Hint: Visualize forces acting in different planes to understand non-coplanarity.
Step 3: Analyze the forces
For a system of forces to be in equilibrium, we can use the concept of vector addition. In three-dimensional space, if we have three non-coplanar forces, they can only balance each other out if there is a fourth force acting on the system.
Hint: Consider how three vectors can be arranged in space and what happens when you try to balance them.
Step 4: Apply the equilibrium condition
According to the equilibrium condition, the resultant of any three forces must equal the opposite of the fourth force. Therefore, to maintain equilibrium with non-coplanar forces, we need at least four forces.
Hint: Think about how adding a fourth force can balance the resultant of the first three.
Step 5: Conclusion
Thus, the minimum number of non-coplanar forces required to keep a particle in equilibrium is 4.
Final Answer: The minimum number of non-coplanar forces that can keep a particle in equilibrium is 4.
A particle is said to be in equilibrium when the net force acting on it is zero. This means that the vector sum of all forces acting on the particle must cancel each other out.
Non-coplanar forces are forces that do not lie in the same plane. This means that these forces act in three-dimensional space.
For a system of forces to be in equilibrium, we can use the concept of vector addition. In three-dimensional space, if we have three non-coplanar forces, they can only balance each other out if there is a fourth force acting on the system.
According to the equilibrium condition, the resultant of any three forces must equal the opposite of the fourth force. Therefore, to maintain equilibrium with non-coplanar forces, we need at least four forces.
Thus, the minimum number of non-coplanar forces required to keep a particle in equilibrium is 4.
Similar Questions
Knowledge Check
Can a couple pair of forces keep the body in equilibrium?
AYesBNoCdata is not givenDNone of the above
Four forces acting on a particle keep it in equilibrium, then :-
View SolutionThe non-directional forces that alters Hardy-Weinberg equilibrium is :
View SolutionP,Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1N , sinθ1=12 , the value of R is
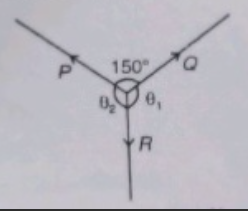
View SolutionP, Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1.9318kg−wt,sinθ1=0.9659, the value of R is (∈kg−wt)
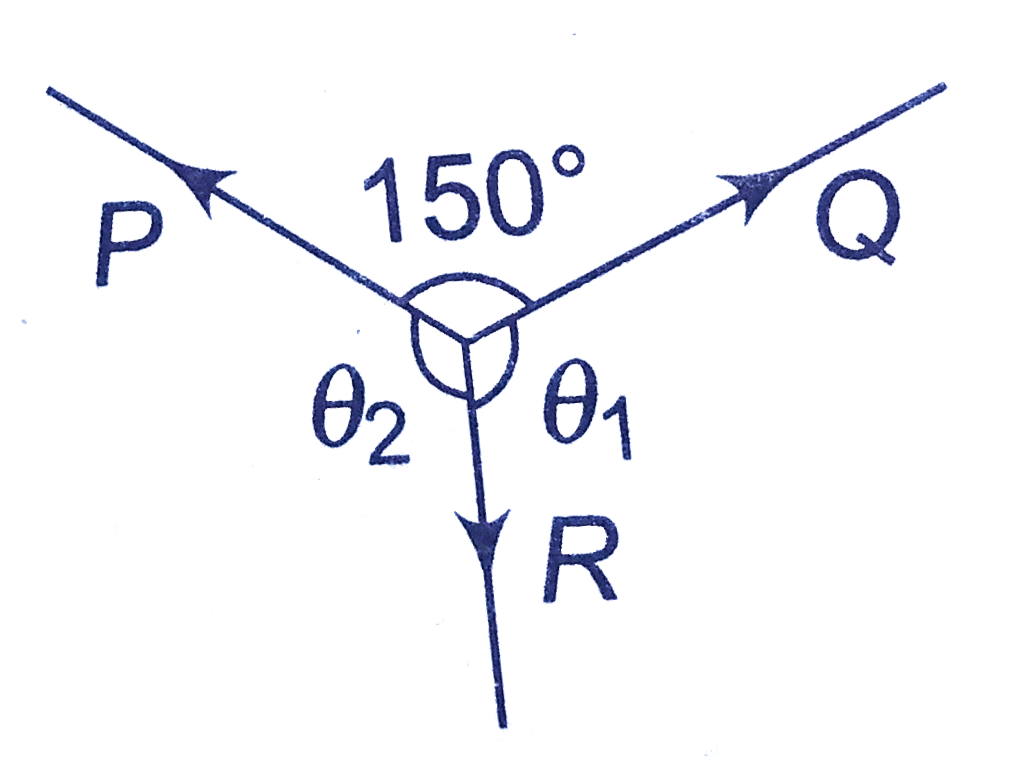
View SolutionP, Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1.9318kg−wt,sinθ1=0.9659, the value of R is (∈kg−wt)
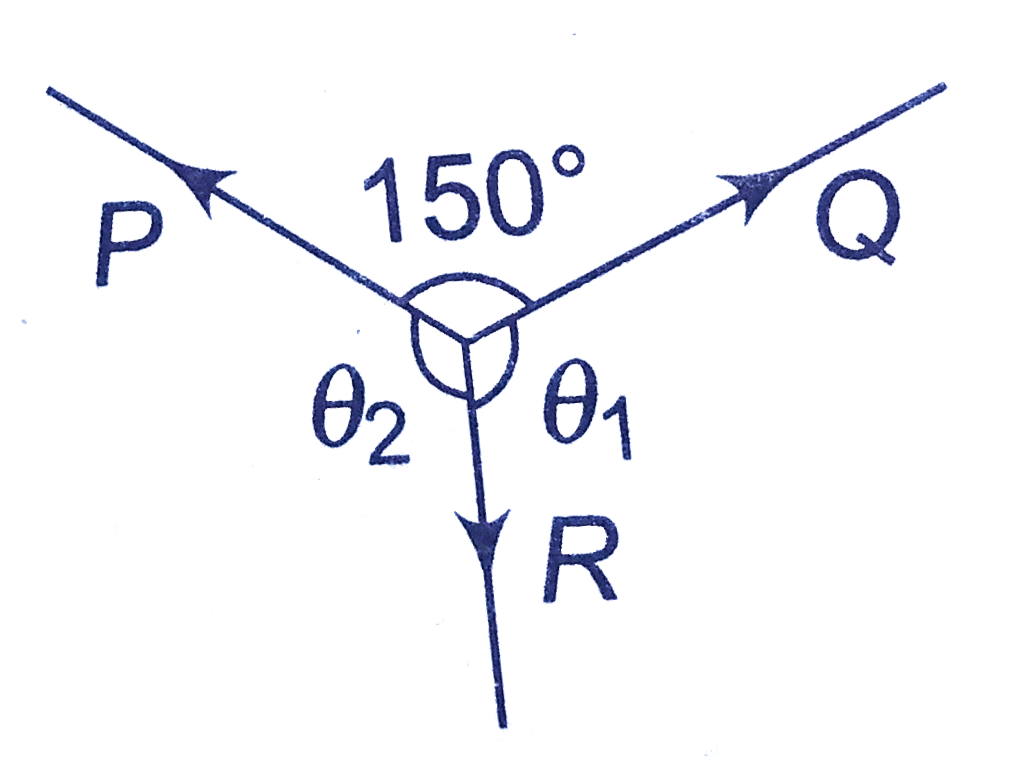
View SolutionFind the minimum height of the obstacle so, that the sphere can stay in equilibrium.

View SolutionA buoy is held inside water contained in a vessel by tying it with a thread to the base of the vessel. Name the three forces that keep the buoy in equilibrium and state the direction in which each force acts.
View Solution
