A person crossing a road with a certain velocity due north sees a car moving towards east The relative velocity of the car w.r.t the person is times that fo the velocity of the persons. The angle made by the relative velocity with the east is
The correct Answer is:B
To solve the problem, we need to analyze the motion of the person and the car in terms of their velocities and the relative velocity between them.
1. Define the Velocities:
- Let the velocity of the person (moving due north) be →vp=u^j.
- Let the velocity of the car (moving due east) be →vc=v^i.
2. Relative Velocity:
- The relative velocity of the car with respect to the person is given by:
→vcp=→vc−→vp=v^i−u^j
3. Magnitude of Relative Velocity:
- The magnitude of the relative velocity |→vcp| can be calculated using the Pythagorean theorem:
|→vcp|=√v2+u2
4. Given Condition:
- According to the problem, the magnitude of the relative velocity is √2 times the velocity of the person:
|→vcp|=√2u
- Therefore, we have:
√v2+u2=√2u
5. Square Both Sides:
- Squaring both sides gives:
v2+u2=2u2
- Simplifying this, we find:
v2=u2
6. Relationship Between Velocities:
- From v2=u2, we conclude that:
v=u
7. Finding the Angle:
- The relative velocity vector can now be expressed as:
→vcp=v^i−v^j=v(^i−^j)
- The angle θ that this vector makes with the east (the positive x-axis) can be found using the tangent function:
tanθ=OppositeAdjacent=vv=1
- Therefore, the angle θ is:
θ=tan−1(1)=45∘
Final Answer:
The angle made by the relative velocity with the east is 45∘.
---
- Let the velocity of the person (moving due north) be →vp=u^j.
- Let the velocity of the car (moving due east) be →vc=v^i.
- The relative velocity of the car with respect to the person is given by:
→vcp=→vc−→vp=v^i−u^j
- The magnitude of the relative velocity |→vcp| can be calculated using the Pythagorean theorem:
|→vcp|=√v2+u2
- According to the problem, the magnitude of the relative velocity is √2 times the velocity of the person:
|→vcp|=√2u
- Therefore, we have:
√v2+u2=√2u
- Squaring both sides gives:
v2+u2=2u2
- Simplifying this, we find:
v2=u2
- From v2=u2, we conclude that:
v=u
- The relative velocity vector can now be expressed as:
→vcp=v^i−v^j=v(^i−^j)
- The angle θ that this vector makes with the east (the positive x-axis) can be found using the tangent function:
tanθ=OppositeAdjacent=vv=1
- Therefore, the angle θ is:
θ=tan−1(1)=45∘
The angle made by the relative velocity with the east is 45∘.
Similar Questions
A car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car is first 25 seconds is
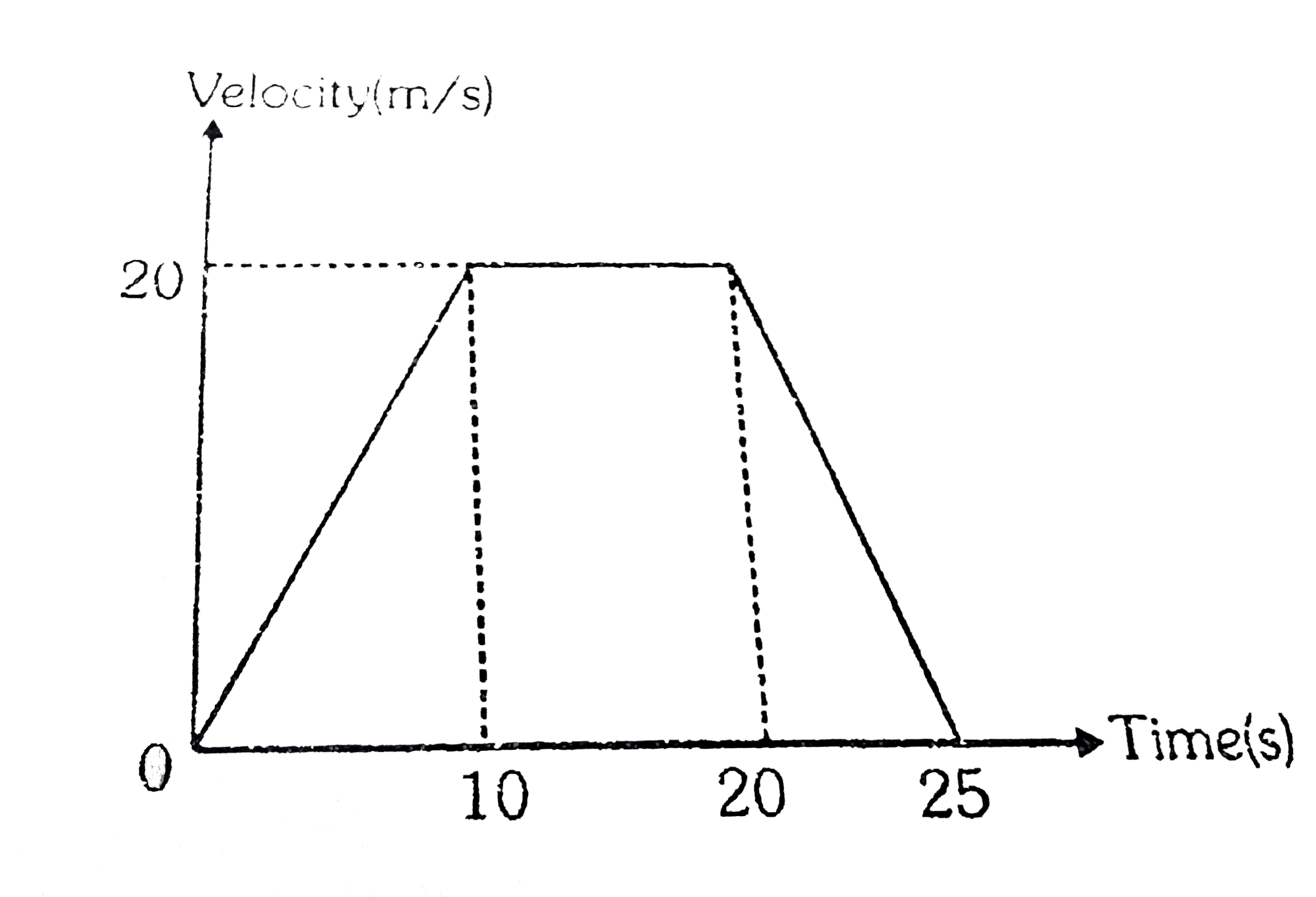
View SolutionThe velocity-time graph of a car moving along a straight road is shown in figure. The average velocity of the car in first 25 seconds is
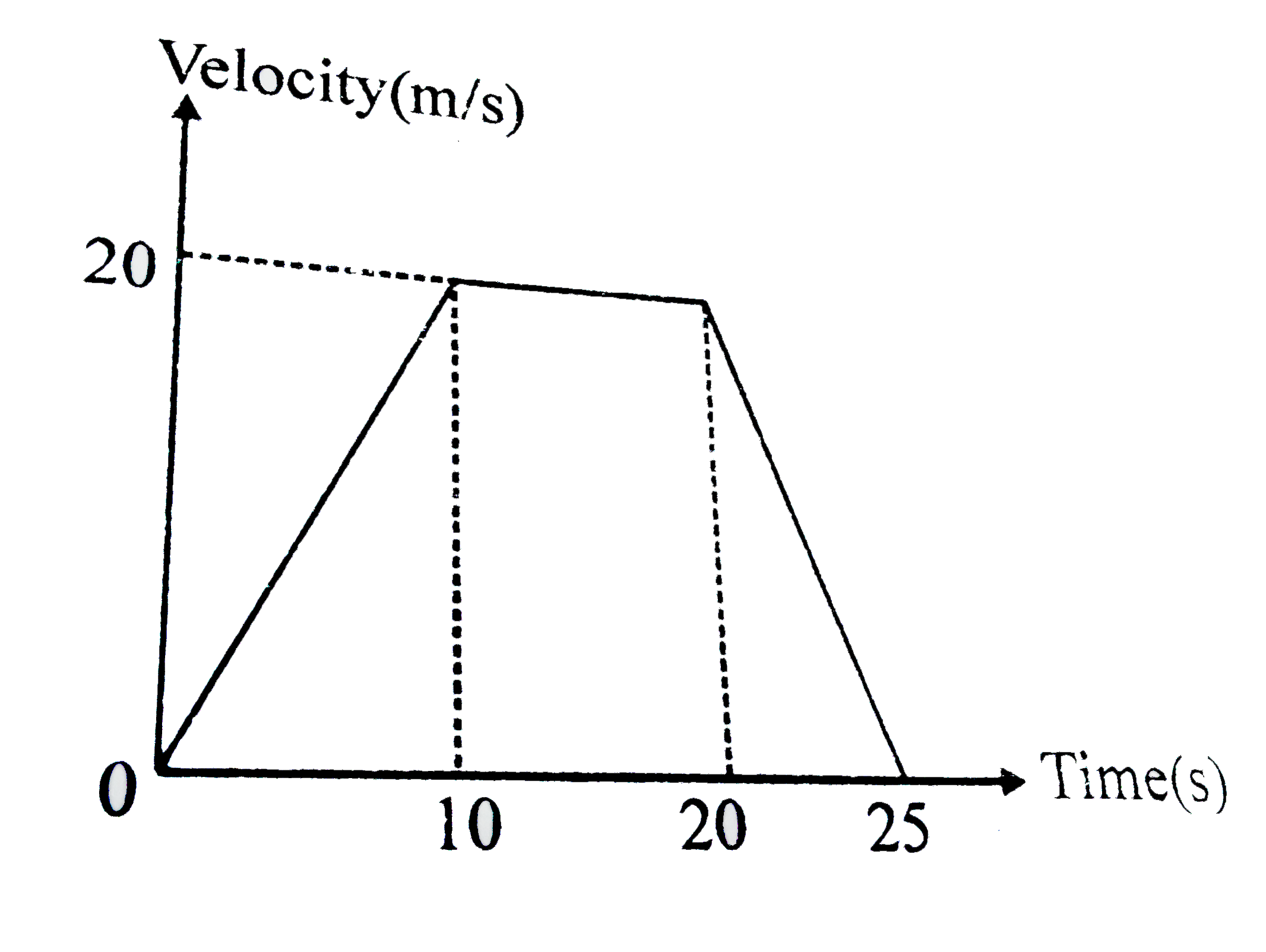
View SolutionA plane mirror and a person are moving towards each other with same velocity v. Then the velocity of the image is
View SolutionThe diagram shows a train moving with constant velocity and a car moving towards the train with constant velocity. The engine driver measures the velocity of the car as v1 . The passenger sitting in the last compartment measures the velocity of the car as v2 . Which of the following statements is true?

View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
View SolutionA person driving a car with a speed 72 km/h suddenly sees a boy crossing the road. If the distance moved by car, before the person applies brakes is 5 m, the reaction time of the person is
View SolutionTwo cars are moving is one a same line dimension in opposite direction with the same speed v. The relative velocity of two cars w.r.t. each other is
View SolutionA motorcylcle is moving with a velocity 80km/hr ahead of a car moving with a velocity of 65 km/hr in the same direction. What is the relative velocity of the motorcyle with respect ot the car:-
View SolutionFind the velocity of the image when a plane mirror and a person are moving towards each other with same velocity v.
View Solution
