A boat takes 4 hr upstream and 2 hr down the stream for covering the same distance. The ratio of velocity of boat to the water in river is
1:3
3:1
1:√3
√3:1
The correct Answer is:B
To solve the problem, we need to find the ratio of the velocity of the boat (VB) to the velocity of the river (VR) based on the time taken to travel upstream and downstream.
1. Understanding Upstream and Downstream:
- When the boat is going upstream, it is moving against the current of the river. Therefore, the effective velocity of the boat upstream (V_upstream) is given by:
Vupstream=VB−VR
- When the boat is going downstream, it is moving with the current of the river. Thus, the effective velocity of the boat downstream (V_downstream) is:
Vdownstream=VB+VR
2. Using Time and Distance:
- Let the distance covered by the boat in both cases be D.
- The time taken to travel upstream is given as 4 hours, and the time taken to travel downstream is given as 2 hours.
- Using the formula Time=DistanceVelocity, we can write:
Upstream: 4=DVB−VR
Downstream: 2=DVB+VR
3. Setting Up Equations:
- From the upstream equation, we can express D:
D=4(VB−VR)
- From the downstream equation, we can express D as well:
D=2(VB+VR)
4. Equating the Two Expressions for Distance:
- Since both expressions equal D, we can set them equal to each other:
4(VB−VR)=2(VB+VR)
5. Expanding and Rearranging:
- Expanding both sides gives:
4VB−4VR=2VB+2VR
- Rearranging the equation:
4VB−2VB=2VR+4VR
2VB=6VR
6. Finding the Ratio:
- Dividing both sides by 2VR gives:
VBVR=62=3
Final Answer:
The ratio of the velocity of the boat to the velocity of the water in the river is:
VBVR=3
- When the boat is going upstream, it is moving against the current of the river. Therefore, the effective velocity of the boat upstream (V_upstream) is given by:
Vupstream=VB−VR
- When the boat is going downstream, it is moving with the current of the river. Thus, the effective velocity of the boat downstream (V_downstream) is:
Vdownstream=VB+VR
- Let the distance covered by the boat in both cases be D.
- The time taken to travel upstream is given as 4 hours, and the time taken to travel downstream is given as 2 hours.
- Using the formula Time=DistanceVelocity, we can write:
Upstream: 4=DVB−VR
Downstream: 2=DVB+VR
- From the upstream equation, we can express D:
D=4(VB−VR)
- From the downstream equation, we can express D as well:
D=2(VB+VR)
- Since both expressions equal D, we can set them equal to each other:
4(VB−VR)=2(VB+VR)
- Expanding both sides gives:
4VB−4VR=2VB+2VR
- Rearranging the equation:
4VB−2VB=2VR+4VR
2VB=6VR
- Dividing both sides by 2VR gives:
VBVR=62=3
The ratio of the velocity of the boat to the velocity of the water in the river is:
VBVR=3
Similar Questions
A river is flowing with velocity 5km/hr as shown in the figure. A boat start from A and reaches the other bank by covering shortest possible distance. Velocity of boat in still water is 3km/hr. The distance boat covers is.

View SolutionA man takes twice as long to row a distance against the stream as to row the same distance in favour of the stream. The ratio of the speed of the boat (in still water) and the stream is :
View Solution
Knowledge Check
A boat travels 16 km upstream in 4hr and 12 km downstream in 6 hr. What is the speed (in km/h) of boat in still water?
A1B2C3D4
A boat goes 12 km upstream and 40 km downstream in 8 hours. It can go 16 km upstream and 32 km downstream in the same time. Find the speed of the boat in still water and the speed of the stream
View SolutionA boat takes 4 hrs to travel certain distance in a river in down stream and it takes 6 hrs to travel the same distance in upstream. Then the time taken by the boat to travel the same distance in still water is
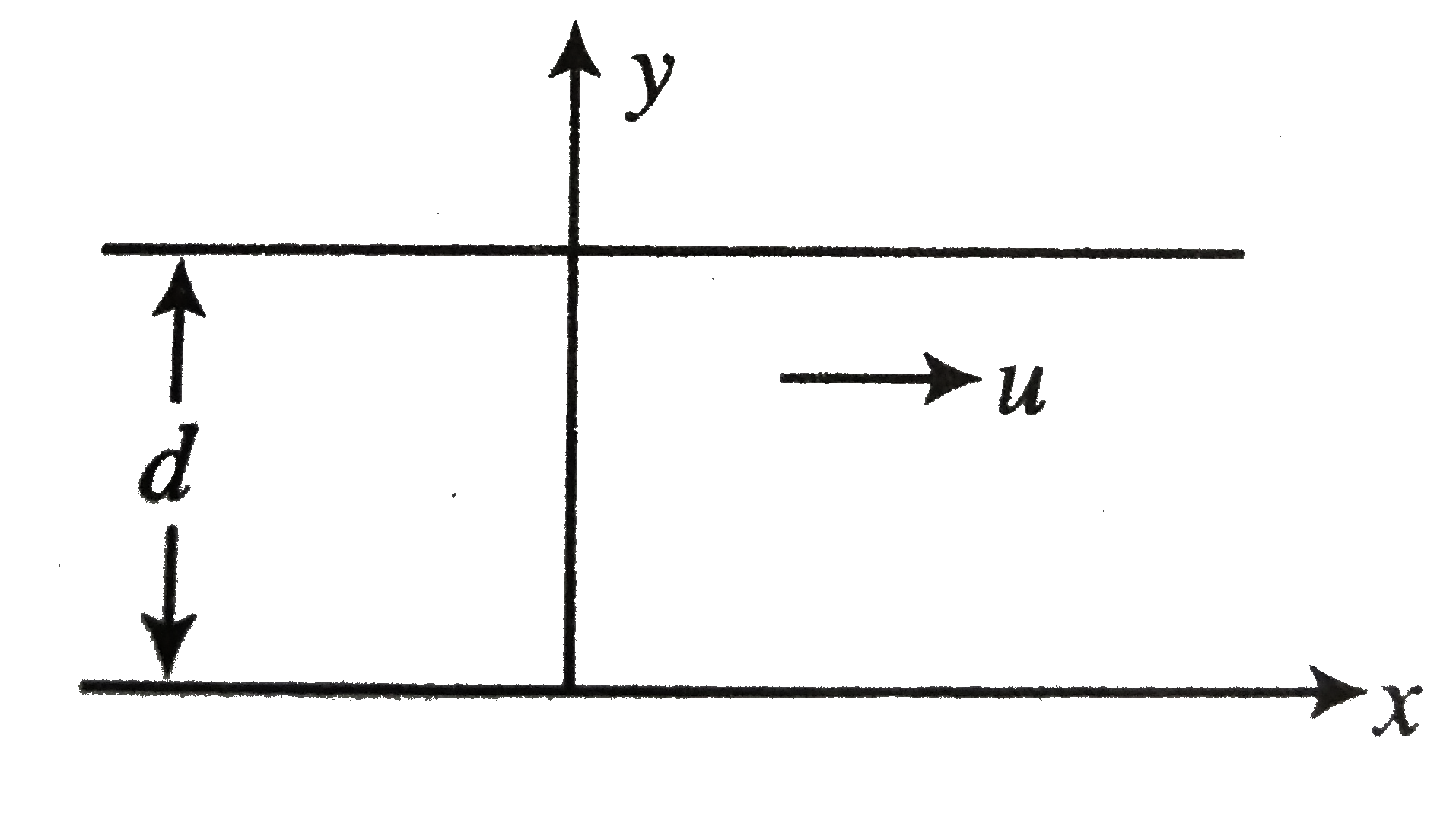
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units. Find time taken by him to across the river.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:

→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionWe know that when a boat travels in water, its net velocity w.r.t. ground is the vector sum of two velocities. First is the velocity of boat itself in river and other is the velocity of water w.r.t. ground. Mathematically:
→vboat=→vboat,water+→vwater.
Now given that velocity of water w.r.t. ground in a river is u. Width of the river is d.
A boat starting from rest aims perpendicular to the river with an acceleration of a = 5t, where t is time. The boat starts from point (1,0) of the coordinate system as shown in figure. Assume SI units.
View SolutionTwo boats A and B moved away from a buoy anchored in the middle of a river along the mutually perpendicular straight lines. A moved along the river and B at fight angle to it Having moves off equal distances from the boy, the boats returned. Find the ratio of the times of motion of the boats, if the velocity of each boat with respect to still water in η=1.2 times greater than the velocity of water current.
View SolutionA man crosses the river perpendicular to river in time t seconds and travels an equal distance down the stream in T seconds. The ratio of man's speed in still water to the river water will be:
View Solution
