A body is projected at an angle 30° with a velocity 42 ms−1 Its maximum height is
22.5m
32.5m
42.5m
52.5m
The correct Answer is:A
To find the maximum height reached by a body projected at an angle, we can use the following steps:
1. Identify the given values:
- Initial velocity u=42m/s
- Angle of projection θ=30∘
- Acceleration due to gravity g=10m/s2 (approximated)
2. Calculate the vertical component of the initial velocity:
The vertical component of the initial velocity uy can be calculated using the sine function:
uy=u⋅sin(θ)=42⋅sin(30∘)
Since sin(30∘)=12:
uy=42⋅12=21m/s
3. Use the kinematic equation to find the maximum height:
At the maximum height, the final vertical velocity vy=0. We can use the kinematic equation:
v2y=u2y+2ayh
Here, ay=−g (since gravity acts downwards), and substituting the values gives:
0=(21)2+2(−10)h
Rearranging this equation to solve for h:
0=441−20h
20h=441
h=44120=22.05m
4. Conclusion:
The maximum height reached by the body is h=22.05m.
- Initial velocity u=42m/s
- Angle of projection θ=30∘
- Acceleration due to gravity g=10m/s2 (approximated)
The vertical component of the initial velocity uy can be calculated using the sine function:
uy=u⋅sin(θ)=42⋅sin(30∘)
Since sin(30∘)=12:
uy=42⋅12=21m/s
At the maximum height, the final vertical velocity vy=0. We can use the kinematic equation:
v2y=u2y+2ayh
Here, ay=−g (since gravity acts downwards), and substituting the values gives:
0=(21)2+2(−10)h
Rearranging this equation to solve for h:
0=441−20h
20h=441
h=44120=22.05m
The maximum height reached by the body is h=22.05m.
Similar Questions
Knowledge Check
A body when projected up with an initial velocity u goes to a maximum height h in time t and then comes back at the point of projection. The correct statement is :
Athe average velocity is 2h/tBthe acceleration is zeroCthe final velocity on reaching the point of projection is 2u.Dthe displacement is zero.
A body is projected at angle 30° to horizontal with a velocity 50 ms−1 .In the above problem range of body is m. [g = 10 ms−2 ]
View SolutionA body is projected with a velocity →v=(3ˆi+4ˆj)ms−1 The maximum height attained by the body is: (g=10ms−2)
View SolutionA body projected with velocity 30 ms−1 reaches its maximum height in 1.5 s. Its range is (g=10ms−2)
View SolutionA body is projected vertically up with u. Its velocity at half its maximum height is
View SolutionA ball is projected at an angle 30° with the horizontal with the velocity 49ms−1. The horizontal range is
View SolutionAt what angle of elevation , should a projectile be projected with velocity with velocity 20ms−1 , so as to reach a maximum height of 10 m ?
View Solution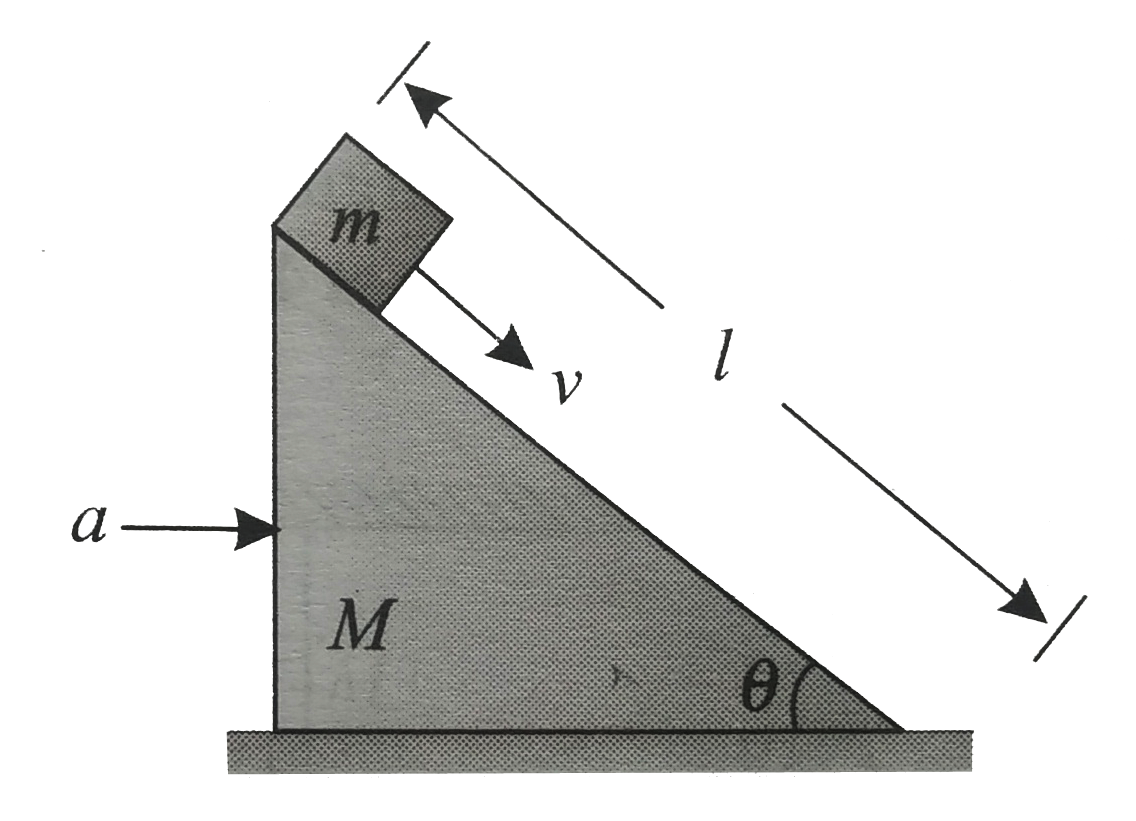
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:
View Solution
