Newton's 2nd law is a local law. It means
i) It is not applicable in non-local area
ii) →F at certain instant determines →a at the same point at that instant
iii) →a at an instant doesnot depend on the history of motion
only (i) is true
only (i) and (ii) are true
only (ii) and (iii) are true
only (i) and (iii) are true
The correct Answer is:C
To solve the question regarding Newton's 2nd law being a local law, we need to analyze each of the provided options and determine which ones are true based on the definition of a local law in physics.
1. Understanding Newton's Second Law:
Newton's Second Law states that the force acting on an object is equal to the mass of that object multiplied by its acceleration (F = ma). This law implies that the acceleration of an object at any given moment is directly related to the net force acting on it at that moment.
2. Analyzing Option (i):
- Statement: "It is not applicable in non-local areas."
- Evaluation: This statement is misleading. Newton's second law is applicable universally, but it is considered a local law because it describes the relationship between force and acceleration at a specific point in time and space. Therefore, this option is incorrect.
3. Analyzing Option (ii):
- Statement: "Force at a certain instant determines acceleration at that same point at that instant."
- Evaluation: This statement is true. According to Newton's second law, the force applied at a specific instant directly determines the acceleration of the object at that same instant. Hence, this option is correct.
4. Analyzing Option (iii):
- Statement: "Acceleration at an instant does not depend on the history of motion."
- Evaluation: This statement is also true. The acceleration of an object at a given moment is determined solely by the net force acting on it at that moment, without regard to any previous forces or accelerations. Thus, this option is correct.
5. Conclusion:
Based on the analysis, the correct interpretations of Newton's second law being a local law are options (ii) and (iii). Therefore, the correct answer is:
- Correct Options: ii) and iii)
Newton's Second Law states that the force acting on an object is equal to the mass of that object multiplied by its acceleration (F = ma). This law implies that the acceleration of an object at any given moment is directly related to the net force acting on it at that moment.
- Statement: "It is not applicable in non-local areas."
- Evaluation: This statement is misleading. Newton's second law is applicable universally, but it is considered a local law because it describes the relationship between force and acceleration at a specific point in time and space. Therefore, this option is incorrect.
- Statement: "Force at a certain instant determines acceleration at that same point at that instant."
- Evaluation: This statement is true. According to Newton's second law, the force applied at a specific instant directly determines the acceleration of the object at that same instant. Hence, this option is correct.
- Statement: "Acceleration at an instant does not depend on the history of motion."
- Evaluation: This statement is also true. The acceleration of an object at a given moment is determined solely by the net force acting on it at that moment, without regard to any previous forces or accelerations. Thus, this option is correct.
Based on the analysis, the correct interpretations of Newton's second law being a local law are options (ii) and (iii). Therefore, the correct answer is:
- Correct Options: ii) and iii)
Similar Questions
The general motion of a rigid body can be considered to be a combination of (i) a motion …. of its centre of mass about an axis, and (ii) its motion about an instantaneous axis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless stick, as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω , the motion at any instant can be taken as a combination of (i) a rotation of the centre of mass of the disc about the z-axis, and (ii) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case.

Now consider two similar systems as shown in the figure: case (a) the disc with its face vertical and parallel to x-z plane, case (b) the disc with its face making an angle of 45° with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the system are rotated with constant angular speed ω about the z-axis
Which of the following statement regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct ?
View SolutionThe general motion of a rigid body can be considered to be a combination of (i) a motion of its centre of mass about an axis, and (ii) its motion about an instantaneous exis passing through the centre of mass. These axes need not be stationary. Consider, for example, a thin uniform disc welded (rigidly fixed) horizontally at its rim to a massless, stick as shown in the figure. When the disc-stick system is rotated about the origin on a horizontal frictionless plane with angular speed ω the motion at any instant can be taken as a combination of (i) a rotation of the disc through an instantaneous vertical axis passing through its centre of mass (as is seen from the changed orientation of points P and Q). Both these motions have the same angular speed ω in this case
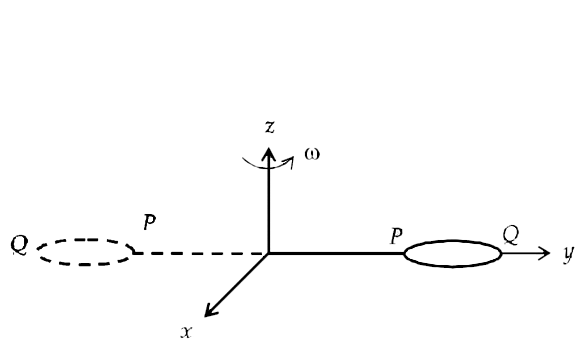
Now consider two similar system as shown in the figure: Case (a) the disc with its face vertical and parallel to x-z plane, Case (b) the disc with its face making an angle of 45∘ with x-y plane and its horizontal diameter parallel to x-axis. In both the cases, the disc is welded at point P, and the systems are rotated with constant angular speed ω about the z-axis.
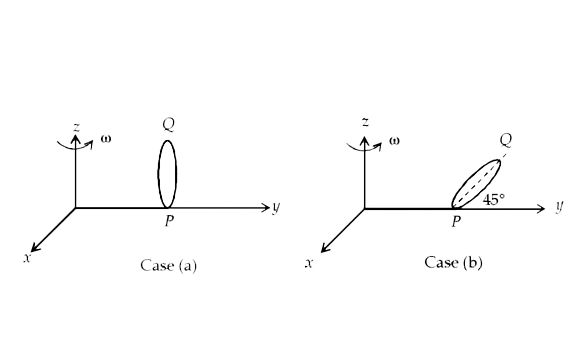
Which of the following statements regarding the angular speed about the instantaneous axis (passing through the centre of mass) is correct?
View SolutionTwo blocks A and B of masses m and 2m respectively are placed on a smooth floor. They are connected by a spring. A third block C of mass m moves with a velocity v0 along the line joing A and B and collides elastically with A, as shown in figure. At a certain instant of time t0 after collision, it is found that the instantaneous velocities of A and B are the same. Further, at this instant the compression of the spring is found to be x0. Determine (i) the common velocity of A and B at time t0, and (ii) the spring constant.
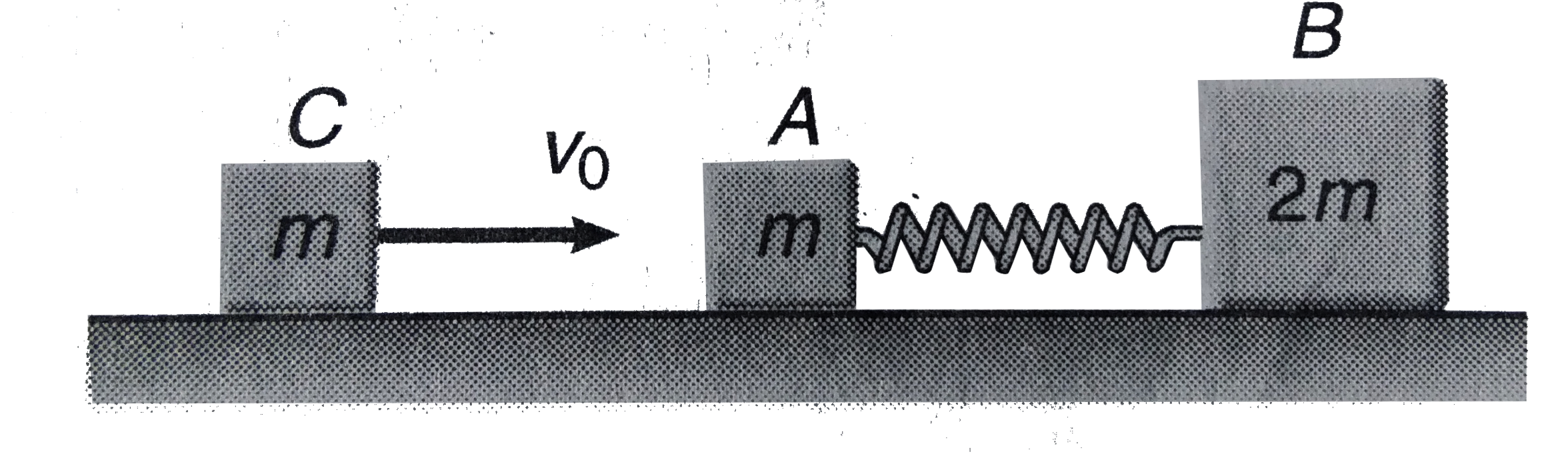
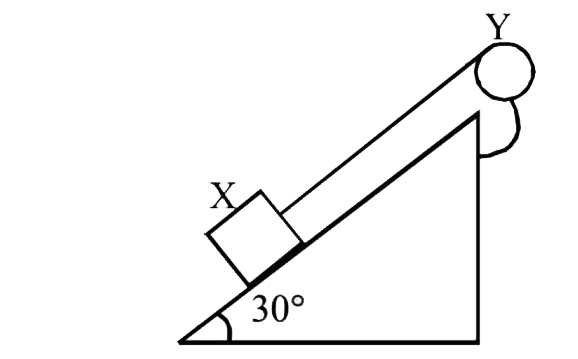
View SolutionA block X of mass 0.5 kg is held by a long massless string on a frictionless inclined plane of inclination 30∘ to the horizontal. The string is wound on a uniform solid cylindrical drum Y of mass 2kg and of radius 0.2m as shown in Fingure. The drum is given an initial angular velocity such that the block X starts moving up the plane.
(i) Find the tension in the string during the motion.
(ii) At a certain instant of time the magnitude of the angular velocity of Y s 10rads−1 calculate the distance travelled by X from that instant of time until it comes to rest
View SolutionA particle is moving in a circular path. The acceleration and momentum vector at an instant of time are →a=2ˆi+3ˆjm/sec2 and →p=6ˆi−4ˆjkgm/sec. Then the motion of the particle is
View SolutionCoulomb's law for electrostatic force between two point charges and Newton's law for gravitational force between two stationary point masses, both have inverse square dependence on the distance between the charges/masees (a) compare the strength of these forces by determining the ratio of their maagnitudes (i) for an electron and as proton (ii) for two protons (b) estimate the accelerations for election and proton due to electrical force of their mutal attraction when they are 1 A apart.
View SolutionTwo coils have self inductances L1=4mHandL2=8mH. Current in both the coils is increasing at same rate. At an instant, when the power given to the two coils is same, find
(i) Ratio of current in the inductors.
(ii) Ratio of potential difference
(iii) Ratio of energy stored
View SolutionA partical of mass 0.2kg undergoes SHM according to the equation x(t)=3sin(πt+π/4).
i. What is the total energy of the partical if potential energy of zero at mean position ?
ii. What are the kinetic and potential energies of partical at time t=1s?
iii. At what time instants is the particals energies purely kinetic?
View SolutionNewton's laws of motion are applicable in all inertial reference frames. Some physical quantities, when measured by observers in different reference frames, have exactly the same value. Such physical quantities are called invariant. In Newtonian mechanics mass, time and force are invariant quantities . On the other hand, some physical quantities, when measured by observer in different reference frames, do not have the same value. Sigmae physical quantities are called not invariant . In Newtonian mechanics displacement, velocity and work ( which is the dot product of force and displacement) are not invariant. Also kinetic energy(=12mv2) is not invariant.
Physicists believe that all laws of physics are invariant in all inertial frames, i.e. the work-energy principle states that the change in the kinetic energy of a particle is equal to the work done on it by the force. Although, work and kinetic energy are not invariant in all reference frames, the work-energy principle remains invariant. Thus even though different observers measuring the motion of the same particle find different values of work and change in kinetic energy, they all find the work energy principle holds in their respective frames.
Choose the invariant quantities from the following
View SolutionNewton's laws of motion are applicable in all inertial reference frames. Some physical quantities, when measured by observers in different reference frames, have exactly the same value. Such physical quantities are called invariant. In Newtonian mechanics mass, time and force are invariant quantities . On the other hand, some physical quantities, when measured by observer in different reference frames, do not have the same value. Sigmae physical quantities are called not invariant . In Newtonian mechanics displacement, velocity and work ( which is the dot product of force and displacement) are not invariant. Also kinetic energy(=12mv2) is not invariant.
Physicists believe that all laws of physics are invariant in all inertial frames, i.e. the work-energy principle states that the change in the kinetic energy of a particle is equal to the work done on it by the force. Although, work and kinetic energy are not invariant in all reference frames, the work-energy principle remains invariant. Thus even though different observers measuring the motion of the same particle find different values of work and change in kinetic energy, they all find the work energy principle holds in their respective frames.
Which of the following quantities is invariant?
View Solution
