A constant force(F) is applied on a stationary particle of mass 'm'. The velocity attained by the particle in a certain displacement will be proportional to
m
1/m
√m
1√m
The correct Answer is:D
To solve the problem, we need to determine how the velocity attained by a particle of mass 'm' under the influence of a constant force 'F' is related to the displacement.
1. Understanding the Force and Mass Relationship:
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=m⋅a
where a is the acceleration of the particle.
2. Expressing Acceleration in Terms of Velocity:
Acceleration can be expressed as the change in velocity over time:
a=dvdt
Thus, we can rewrite the force equation as:
F=m⋅dvdt
3. Using the Chain Rule:
We can express acceleration in terms of displacement x as follows:
a=dvdt=dvdx⋅dxdt
Here, dxdt is the velocity v. Therefore, we can rewrite the force equation:
F=m⋅v⋅dvdx
4. Rearranging the Equation:
Rearranging gives us:
Fm⋅dx=v⋅dv
5. Integrating Both Sides:
Now, we integrate both sides. The left side integrates with respect to x and the right side with respect to v:
∫Fmdx=∫vdv
This results in:
Fm⋅x=v22+C
Assuming the initial velocity is zero (the particle starts from rest), the constant C will be zero.
6. Solving for Velocity:
Thus, we have:
Fm⋅x=v22
Rearranging gives:
v2=2Fxm
Taking the square root of both sides results in:
v=√2Fxm
7. Determining Proportionality:
From the equation v=√2Fxm, we can see that the velocity v is directly proportional to the square root of the displacement x and the force F, and inversely proportional to the square root of the mass m.
Conclusion:
Thus, the velocity attained by the particle in a certain displacement is proportional to:
v∝√Fm⋅√x
According to Newton's second law, the net force acting on an object is equal to the mass of the object multiplied by its acceleration:
F=m⋅a
where a is the acceleration of the particle.
Acceleration can be expressed as the change in velocity over time:
a=dvdt
Thus, we can rewrite the force equation as:
F=m⋅dvdt
We can express acceleration in terms of displacement x as follows:
a=dvdt=dvdx⋅dxdt
Here, dxdt is the velocity v. Therefore, we can rewrite the force equation:
F=m⋅v⋅dvdx
Rearranging gives us:
Fm⋅dx=v⋅dv
Now, we integrate both sides. The left side integrates with respect to x and the right side with respect to v:
∫Fmdx=∫vdv
This results in:
Fm⋅x=v22+C
Assuming the initial velocity is zero (the particle starts from rest), the constant C will be zero.
Thus, we have:
Fm⋅x=v22
Rearranging gives:
v2=2Fxm
Taking the square root of both sides results in:
v=√2Fxm
From the equation v=√2Fxm, we can see that the velocity v is directly proportional to the square root of the displacement x and the force F, and inversely proportional to the square root of the mass m.
Thus, the velocity attained by the particle in a certain displacement is proportional to:
v∝√Fm⋅√x
Similar Questions
A constant force(F) is applied on a stationary particle of mass 'm'. the velocity attained by the particle in a certain interval of time will be proportional to
View SolutionA constant force (F) is applied on a stationary particle of mass m, the velocity attained by the particle in a certain interval of time will be proportional to
View Solution
Knowledge Check
The escape velocity of a particle of mass 'm'
Avaries as m2Bvaries as mCvaries as m−1Dis independent of mass
A constant power P is applied on a particle of mass m. find kintic energy, velocity and displacement of particle as function of time t.
View SolutionA constant power P is applied to a particle of mass m. The distance traveled by the particle when its velocity increases from v1 to v2 is (neglect friction):
View SolutionA constant force acts on a mass m at rest. Velocity acquired in travelling a fixed distance is directly proportional to :
View Solutionvelocity time graph of a particle is shown in figure. Find displacement of the particle.
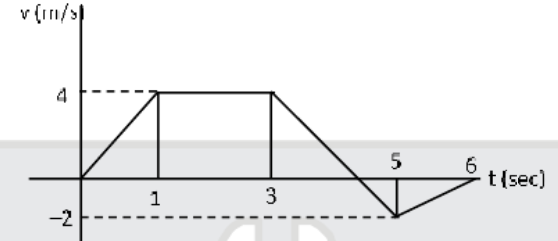
View SolutionA person applies a constant force →F on a particle of mass m and finds tht the particle movs in a circle of radius r with a uniform speed v as seen from an inertial frame of reference.
View SolutionThe escape velocity of a particle of mass m varies as
View SolutionA particle of mass 1 kg has a velocity of 2m/s. A constant force of 2N acts on the particle for 1s in a direction perpendicular to its initial velocity. Find the velocity and displacement of the particle at the end of 1 s.
View Solution
