(A) : A body subjected to three concurrent forces cannot be in equilibrium.
(R) : If large number of concurrent forces acting on the same point, then the point may be in equilibrium, even if the vectorial sum of all the force is not zero.
Both (A) and (R) are true and (R) is the correct explanation of (A)
Both (A) and (R) are true and (R) is not the correct explanation of A
(A) is false but ( R) is True
Both (A) and (R ) are false
The correct Answer is:D
To solve the question, we need to analyze both the assertion (A) and the reason (R) provided.
Step 1: Analyze the Assertion (A)
The assertion states: "A body subjected to three concurrent forces cannot be in equilibrium."
- For a body to be in equilibrium, the vector sum of all forces acting on it must be zero.
- It is possible for three concurrent forces to be in equilibrium if they are balanced. For example, if one force acts in one direction and the other two forces are equal in magnitude and act in opposite directions, the net force will be zero.
Conclusion for Assertion (A): This statement is false because a body can be in equilibrium under three concurrent forces if they balance each other out.
Step 2: Analyze the Reason (R)
The reason states: "If a large number of concurrent forces are acting on the same point, then the point may be in equilibrium, even if the vectorial sum of all the forces is not zero."
- This statement is also incorrect. For any number of concurrent forces acting on a point, for the body to be in equilibrium, the vector sum of all those forces must be zero. If the vector sum is not zero, the body cannot be in equilibrium.
Conclusion for Reason (R): This statement is false because equilibrium requires the vector sum of all forces to be zero, regardless of the number of forces.
Final Conclusion
Since both the assertion (A) and the reason (R) are false, the correct answer is: Option D: Both A and R are false.
---
The assertion states: "A body subjected to three concurrent forces cannot be in equilibrium."
- It is possible for three concurrent forces to be in equilibrium if they are balanced. For example, if one force acts in one direction and the other two forces are equal in magnitude and act in opposite directions, the net force will be zero.
Conclusion for Assertion (A): This statement is false because a body can be in equilibrium under three concurrent forces if they balance each other out.
The reason states: "If a large number of concurrent forces are acting on the same point, then the point may be in equilibrium, even if the vectorial sum of all the forces is not zero."
Conclusion for Reason (R): This statement is false because equilibrium requires the vector sum of all forces to be zero, regardless of the number of forces.
Since both the assertion (A) and the reason (R) are false, the correct answer is: Option D: Both A and R are false.
Similar Questions
Knowledge Check
A body subjected to three concurrent force is found to be in equilibrium. The resultant of any two force
Ais equal to third forceBis equal to third forceCis collinear fifth the third forceDall of these
Which of the following sets of concurrent force may be in equilibrium?
View SolutionWhich of the following sets of concurrent force may be in equilibrium?
View SolutionWhich of the following group of concurrent forces may be in equilibrium (R=0)?
View SolutionThree forces are acting on a body to make it in equilibrium , which set can not do it ?
View SolutionIf four forces act at a point 'O' as shown in the figure and if O is in equilibrium then the value of 'θ' & 'P' are
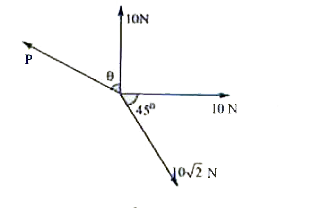
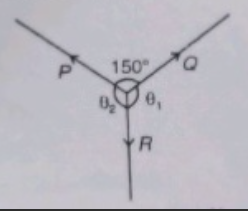
View SolutionP,Q and R are three coplanar forces acting at a point and are in equilibrium. Given P=1N , sinθ1=12 , the value of R is
View SolutionMoment of concurrent forces about any point is constant.
If vector sum of all concurrent forces is zero, then moment of all the forces about any point is also zero.
View Solution