A gun of mass M fires a bullet of mass m with a Kinetic energy E. The velocity of recoil of the gun is
√2MEm
√2mEM
√2mEM+m
√2MEM+m
The correct Answer is:B
To find the velocity of recoil of the gun when it fires a bullet, we can follow these steps:
Step 1: Understand the given information
- Mass of the gun = M
- Mass of the bullet = m
- Kinetic energy of the bullet = E
Step 2: Relate kinetic energy to the velocity of the bullet
The kinetic energy E of the bullet can be expressed using the formula:
E=12mv2
where v is the velocity of the bullet.
Step 3: Solve for the velocity of the bullet
Rearranging the kinetic energy formula to solve for v:
v2=2Em
Taking the square root of both sides gives:
v=√2Em(1)
Step 4: Apply the conservation of momentum
According to the law of conservation of momentum, the total momentum before firing must equal the total momentum after firing. Initially, both the gun and bullet are at rest, so:
0=mv+MV′
where V′ is the recoil velocity of the gun.
Step 5: Set up the momentum equation
From the conservation of momentum:
0=mv+MV′
Rearranging gives:
MV′=−mv
Thus, we can express the velocity of the gun as:
V′=−mMv(2)
Step 6: Substitute the expression for v from Step 3 into the momentum equation
Substituting equation (1) into equation (2):
V′=−mM√2Em
This simplifies to:
V′=−√2EmM(3)
Step 7: Interpret the result
The negative sign indicates that the direction of the recoil velocity V′ of the gun is opposite to the direction of the bullet's velocity.
Final Result
The velocity of recoil of the gun is:
V′=−√2EmM
- Mass of the gun = M
- Mass of the bullet = m
- Kinetic energy of the bullet = E
The kinetic energy E of the bullet can be expressed using the formula:
E=12mv2
where v is the velocity of the bullet.
Rearranging the kinetic energy formula to solve for v:
v2=2Em
Taking the square root of both sides gives:
v=√2Em(1)
According to the law of conservation of momentum, the total momentum before firing must equal the total momentum after firing. Initially, both the gun and bullet are at rest, so:
0=mv+MV′
where V′ is the recoil velocity of the gun.
From the conservation of momentum:
0=mv+MV′
Rearranging gives:
MV′=−mv
Thus, we can express the velocity of the gun as:
V′=−mMv(2)
Substituting equation (1) into equation (2):
V′=−mM√2Em
This simplifies to:
V′=−√2EmM(3)
The negative sign indicates that the direction of the recoil velocity V′ of the gun is opposite to the direction of the bullet's velocity.
The velocity of recoil of the gun is:
V′=−√2EmM
Similar Questions
A gun of mass M fires a bullet of mass m, with a Kinetic energy E. The total kinetic energy in the firing process is
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA loaded spring gun of mass M fires a bullet of mass m with a velocity v at an angle of elevation θ. The gun is initially at rest on a horizontal smooth surface. After firing, the centre of mass of the gun and bullet system
View SolutionA gun of mass M fires a bullet of mass m with a velocity v relative to the gun. The average force required to bring the gun to rest in 0.5 sec. is
View SolutionA gun of mass M fires a bullet of mass m with a horizontal speed V. The gun is fitted with a concave mirror of focal length f facing towards the receding bullet. Find the speed of separation of the bullet and the image just after the gun was fired.
View SolutionA gun of mass m1 fires a bullet of mass m2 with a horizontal speed
v0. The gun is fitted with a concave mirror of focal length f facing towards a
receding bullet.Find the speed of separations of the bullet and the image just after the gun was fired.
View SolutionChoose the correct option:
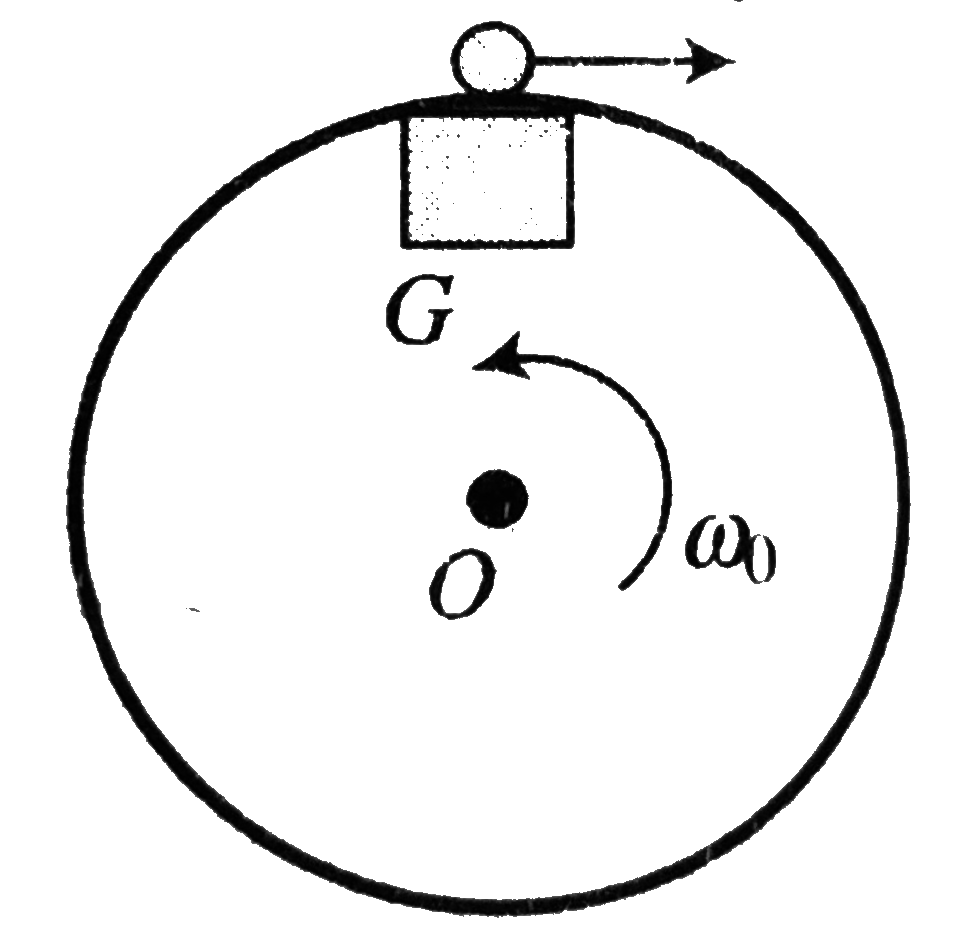
A horizontal turn table in the form of a disc of radius r carries a gun at G and rotates with angular velocity ω0 about a vertical axis passing through the centre O. The increase in angular velocity of the system if the gun fires a bullet of mass m with a tangential velocity v with respect to the gun is (moment of inertia of gun + table about O is I0)
View SolutionA gun of mass M. fires a shell of mass m horizontally and the energy of explosion is such as would be sufficient to project the shell vertically to a height 'h' . The recoil velocity of the gun is
View SolutionA gun of mass 10kg fires 4 bullets per second. The mass of each bullet is 20 g and the velocity of the bullet when it leaves the gun is 300ms−1. The force required to hold the gun while firing is
View SolutionIf , a machine gun fires n bullets per second each with kinetic energy K, then the power of the machine gun is
View Solution
