A boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
472 N
435 N
232 N
568 N
The correct Answer is:A
To solve the problem of finding the tension in the rope when a boy of mass 40 kg climbs up with an acceleration of 2 m/s², we can follow these steps:
Step 1: Identify the Forces Acting on the Boy
When the boy climbs up, two main forces act on him:
1. The gravitational force (weight) acting downward, which is given by W=mg.
2. The tension T in the rope acting upward.
Step 2: Write Down the Known Values
- Mass of the boy, m=40kg
- Acceleration of the boy, a=2m/s2
- Acceleration due to gravity, g=9.8m/s2
Step 3: Set Up the Equation of Motion
Since the boy is climbing up with an acceleration, we can apply Newton's second law. The net force acting on the boy can be expressed as:
T−mg=ma
Where:
- T is the tension in the rope,
- mg is the weight of the boy,
- ma is the net force due to the upward acceleration.
Step 4: Rearrange the Equation to Solve for Tension
Rearranging the equation gives us:
T=mg+ma
Step 5: Substitute the Known Values
Now we can substitute the known values into the equation:
T=m(g+a)
T=40kg×(9.8m/s2+2m/s2)
T=40kg×11.8m/s2
Step 6: Calculate the Tension
Now we perform the multiplication:
T=40×11.8=472N
Conclusion
The tension in the rope is 472N.
---
When the boy climbs up, two main forces act on him:
1. The gravitational force (weight) acting downward, which is given by W=mg.
2. The tension T in the rope acting upward.
- Mass of the boy, m=40kg
- Acceleration of the boy, a=2m/s2
- Acceleration due to gravity, g=9.8m/s2
Since the boy is climbing up with an acceleration, we can apply Newton's second law. The net force acting on the boy can be expressed as:
T−mg=ma
Where:
- T is the tension in the rope,
- mg is the weight of the boy,
- ma is the net force due to the upward acceleration.
Rearranging the equation gives us:
T=mg+ma
Now we can substitute the known values into the equation:
T=m(g+a)
T=40kg×(9.8m/s2+2m/s2)
T=40kg×11.8m/s2
Now we perform the multiplication:
T=40×11.8=472N
The tension in the rope is 472N.
Similar Questions
A can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with an acceleration of 1m/s2, what must be the tension in the rope ?
View SolutionTow men of masses m1andm2 hold on the opposite ends of a rope passing over a frictionless pulley. The men m1 climbs up the pore with an acceleration of 1.2m/s2 relative to the rope. The mann m2 climbs up the rope with an acceleration of 2m/s2 relative to the rope. Find the tension in the rope if m140kgandm2=60kg. Also find the time after the time after which they will be at same horizontal level if they start from rest and are initially separted by 5 m.
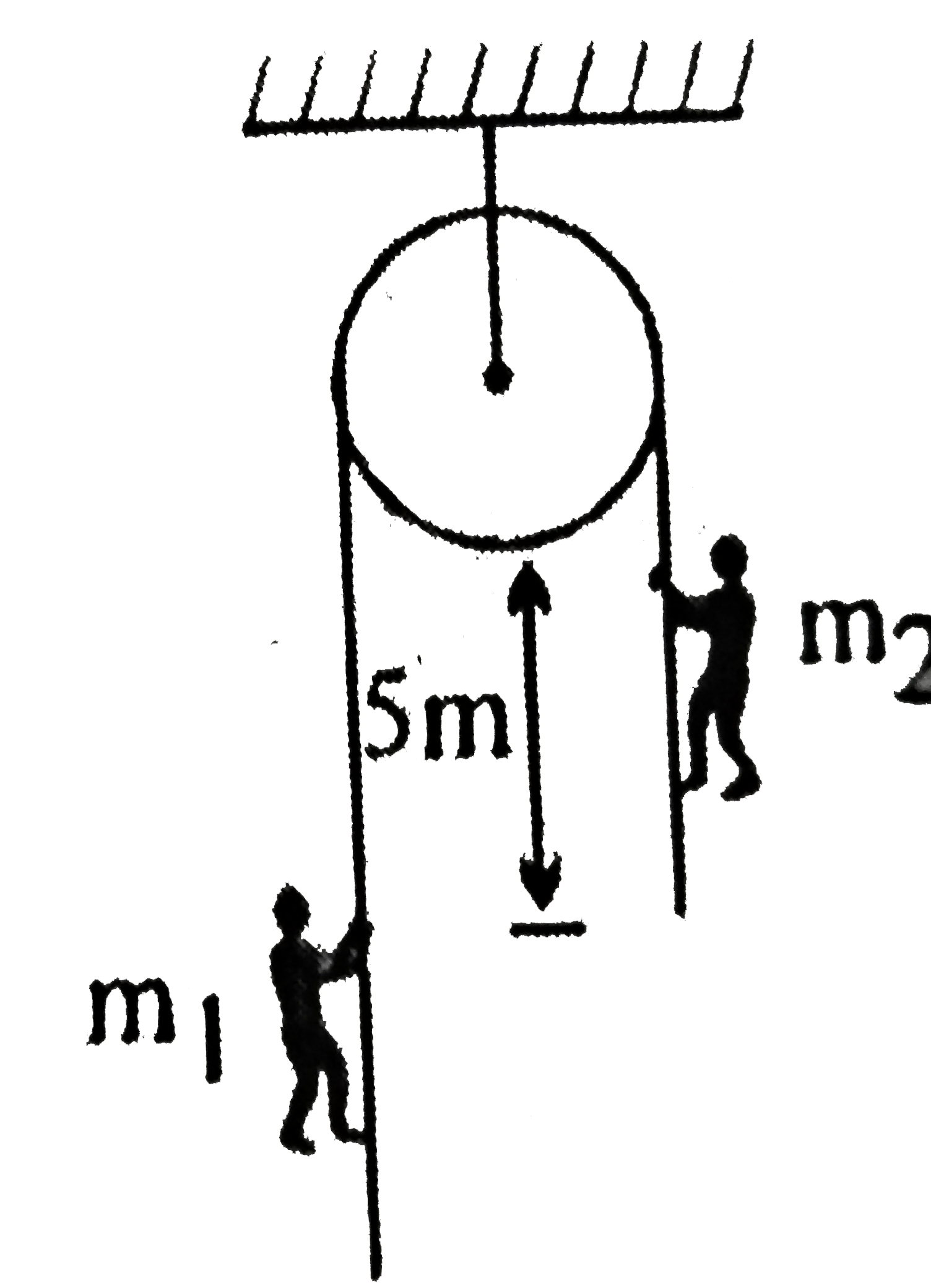
View Solution
Knowledge Check
A mass of 1 kg is suspended by means of a thread. The system is (i) lifted up with an acceleration of 4.9ms2 (ii) lowered with an acceleration of 4.9ms−2. The ratio of tension in the first and second case is
A3:1B1:2C1:3D2:1
A can of paint with a mass of 6 kg hangs from a rope. If the can is to be pulled up to a rooftop with an acceleration of 1m/s, what must be the tension in the rope ?
View SolutionA balloon of mass 10 kg is raising up with an acceleration of 20ms−2. If a mass of 4 kg is removed from the balloon its acceleration becomes ( take, g=10ms−2)
View SolutionA uniform rope of mass m hangs freely from a ceiling. A bird of mass M climbs up the rope with an acceleration a. The force exerted by the rope on the ceiling is
View SolutionTwo monkey of masses 10 kg and 8 kg are moving along a verticle rope as shown in fig. the former climbing up with an acceleration of 2ms−2, while the later coming down with a uniform velocity of 2ms−2. Find the tension in the rope at the fixed support.

View SolutionTwo blocks shown in figure are connected by a heavy uniform rope of mass 4kg. An upward force of 200N is applied as shown
(a) What is the acceleration of the system .
(b)What is the tension at the top of the rope ?
( c) What is the tension at the mid- point of the rop
(Takeg=9.8m/s2)

View SolutionA monkey of mass 40 kg climbs on a rope which can withstand a maximum tension of 600 N In which of the following cases will the rope break : The monkey
(a) climbs up with an acceleration of 6ms−2
(b) climbs down with an acceleration of 4ms−2
(c) climbs up with a uniform speed of 5ms−1
(d) falls down the rope nearly freely under gravity ? (Ignore the mass of the rope.)
View SolutionIn order to raise a mass of 100 kg, a man of mass 60 kg fastens a rope to it and passes the rope over a smooth pulley. He climbs the rope with acceleration 5g/4 relative to the rope. The tension in the rope is (take g=10ms−2)

View Solution
