A block of mass 2kg is lying on a rough inclined plane. The force needed to move the block up the plane with uniform velocity by applying a force parallel to the plane is 100N. The force needed to move the block up with an accele-ration of 2ms−2 is
100 N
200 N
96 N
104 N
The correct Answer is:D
To solve the problem step by step, we need to analyze the forces acting on the block on the inclined plane.
Step 1: Understanding the Forces
The block of mass m=2kg is on a rough inclined plane. The forces acting on the block include:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force f acting down the plane (since the block is on a rough surface).
- The applied force F acting parallel to the inclined plane.
Step 2: Forces when moving with uniform velocity
When the block is moving with uniform velocity, it is in equilibrium in the direction parallel to the incline. The force needed to move the block up the plane with uniform velocity is given as F=100N. This means:
F−mgsinθ−f=0
From this, we can conclude that:
mgsinθ+f=100N
Step 3: Forces when moving with acceleration
Now, when the block is moving up the incline with an acceleration a=2m/s2, we can use Newton's second law:
F−mgsinθ−f=ma
Substituting ma with 2m (since m=2kg):
F−mgsinθ−f=2m
F−mgsinθ−f=2×2
F−mgsinθ−f=4
Step 4: Relating the two scenarios
From the first scenario, we have:
mgsinθ+f=100N
We can express f as:
f=100−mgsinθ
Now, substituting this expression for f into the second equation:
F−mgsinθ−(100−mgsinθ)=4
This simplifies to:
F−100=4
Thus, we find:
F=104N
Conclusion
The force needed to move the block up the inclined plane with an acceleration of 2m/s2 is 104N.
The block of mass m=2kg is on a rough inclined plane. The forces acting on the block include:
- The gravitational force mg acting downwards.
- The normal force N acting perpendicular to the inclined plane.
- The frictional force f acting down the plane (since the block is on a rough surface).
- The applied force F acting parallel to the inclined plane.
When the block is moving with uniform velocity, it is in equilibrium in the direction parallel to the incline. The force needed to move the block up the plane with uniform velocity is given as F=100N. This means:
F−mgsinθ−f=0
From this, we can conclude that:
mgsinθ+f=100N
Now, when the block is moving up the incline with an acceleration a=2m/s2, we can use Newton's second law:
F−mgsinθ−f=ma
Substituting ma with 2m (since m=2kg):
F−mgsinθ−f=2m
F−mgsinθ−f=2×2
F−mgsinθ−f=4
From the first scenario, we have:
mgsinθ+f=100N
We can express f as:
f=100−mgsinθ
F−mgsinθ−(100−mgsinθ)=4
This simplifies to:
F−100=4
Thus, we find:
F=104N
The force needed to move the block up the inclined plane with an acceleration of 2m/s2 is 104N.
Similar Questions
Knowledge Check
A block of mass m is on an inclined plane of angle θ. The coefficient of friction between the block and the plane is μ and tanθ>μ. The block is held stationary by applying a force P parallel to the plane. The direction of force pointing up the plane is taken to be positive. As P is varied from P1=mg(sinθ−μcosθ) to P2=mg(sinθ+μcosθ), the frictional force f versus P graph will look like
A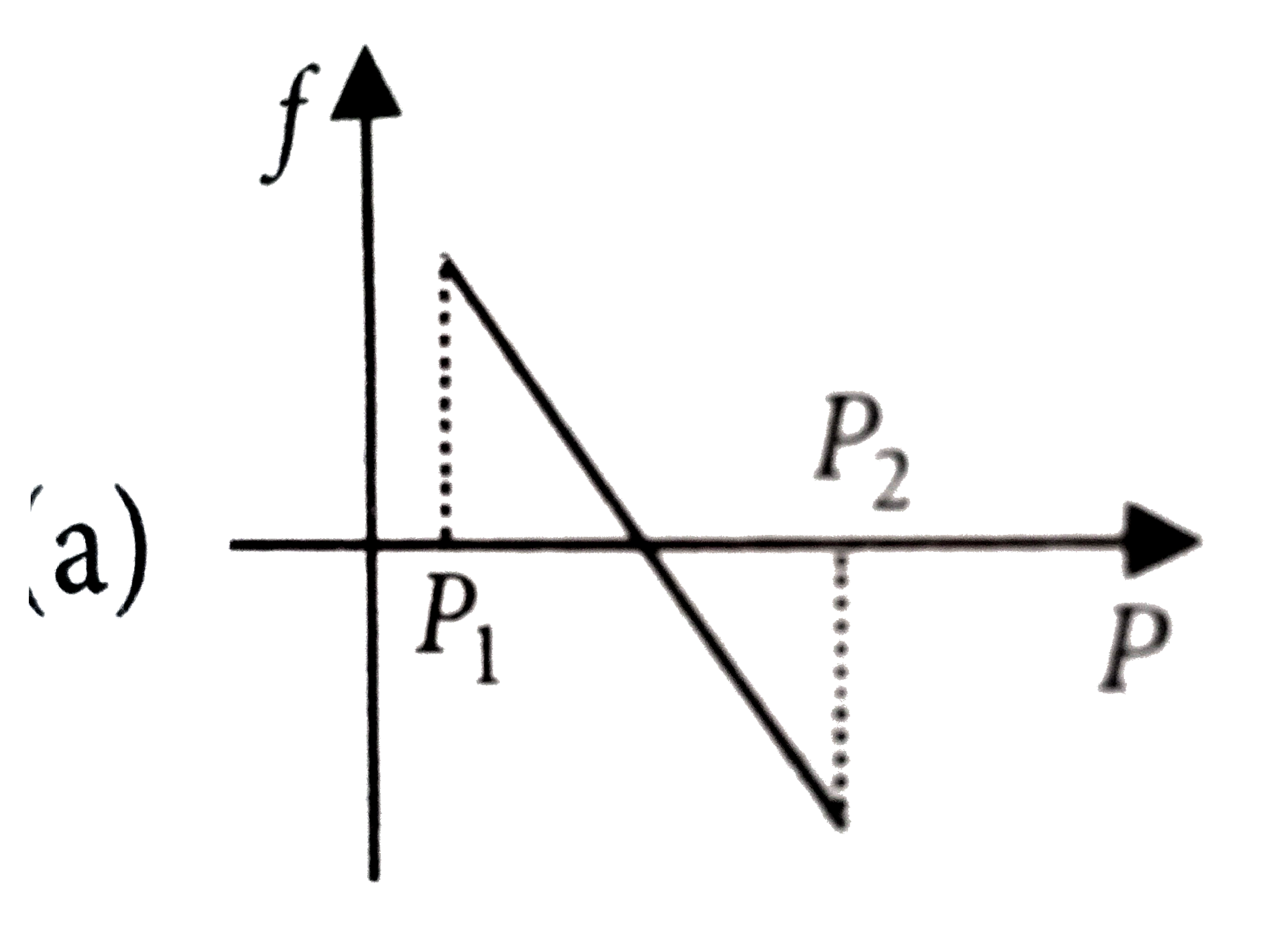 B
B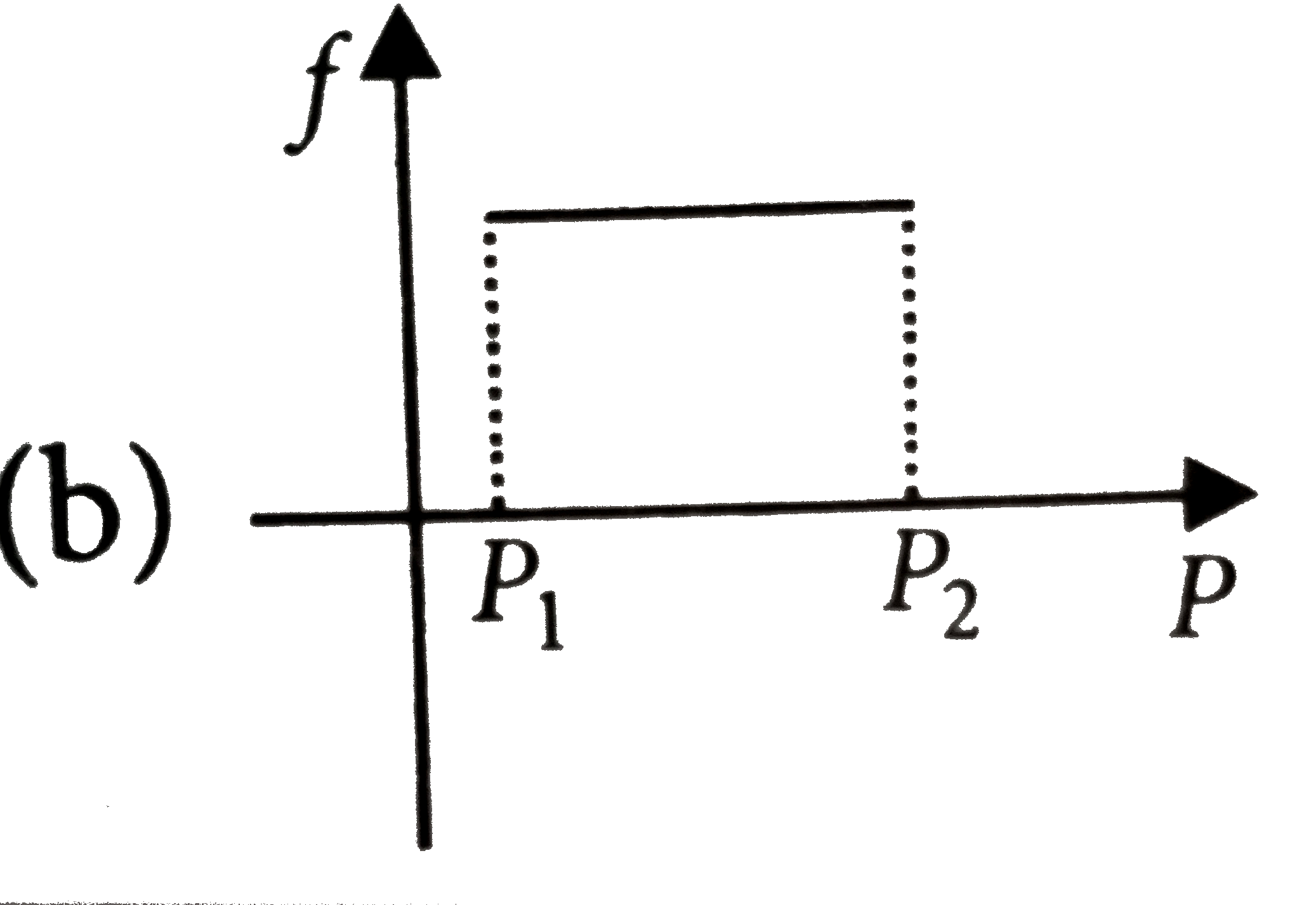 C
C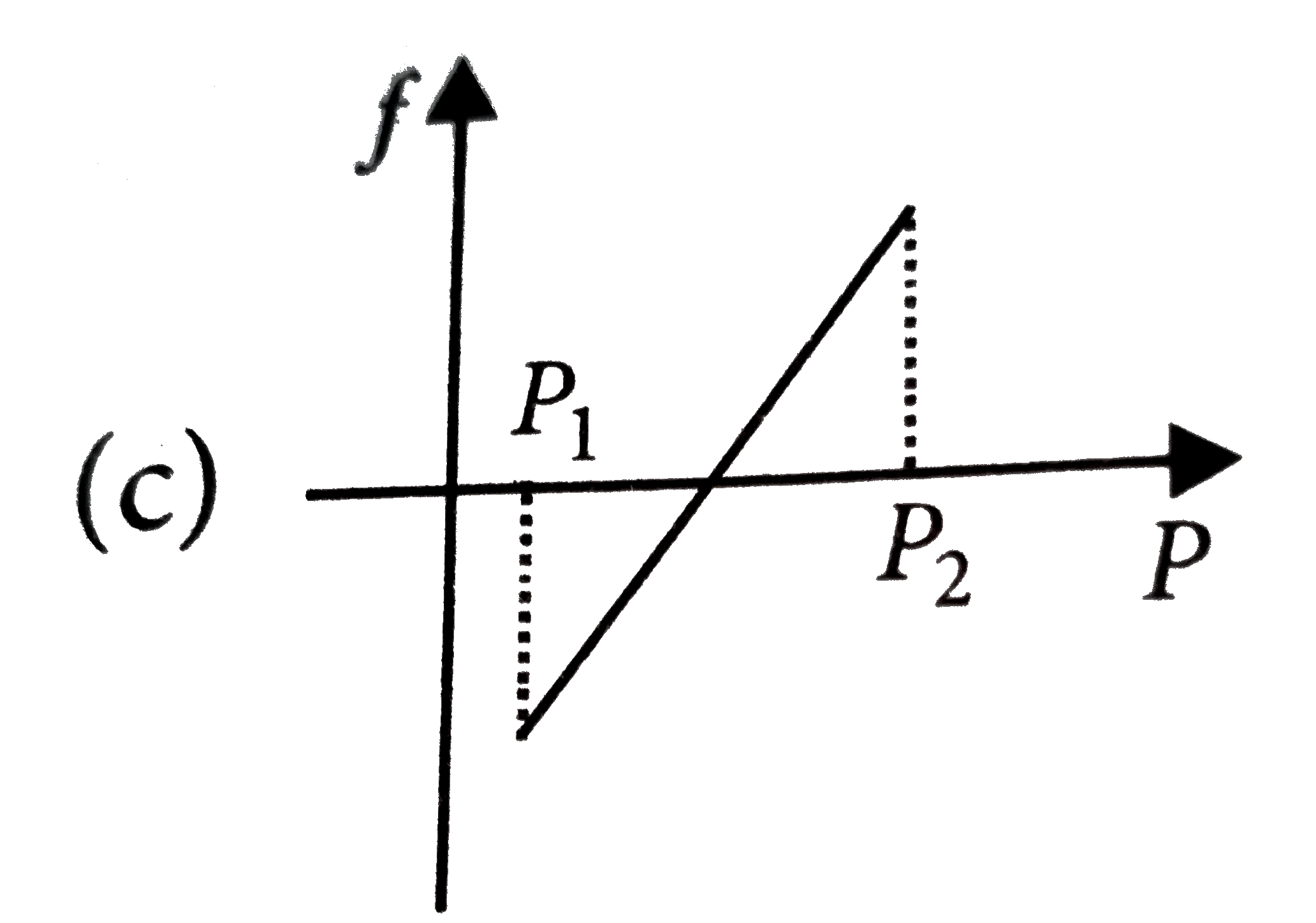 D
D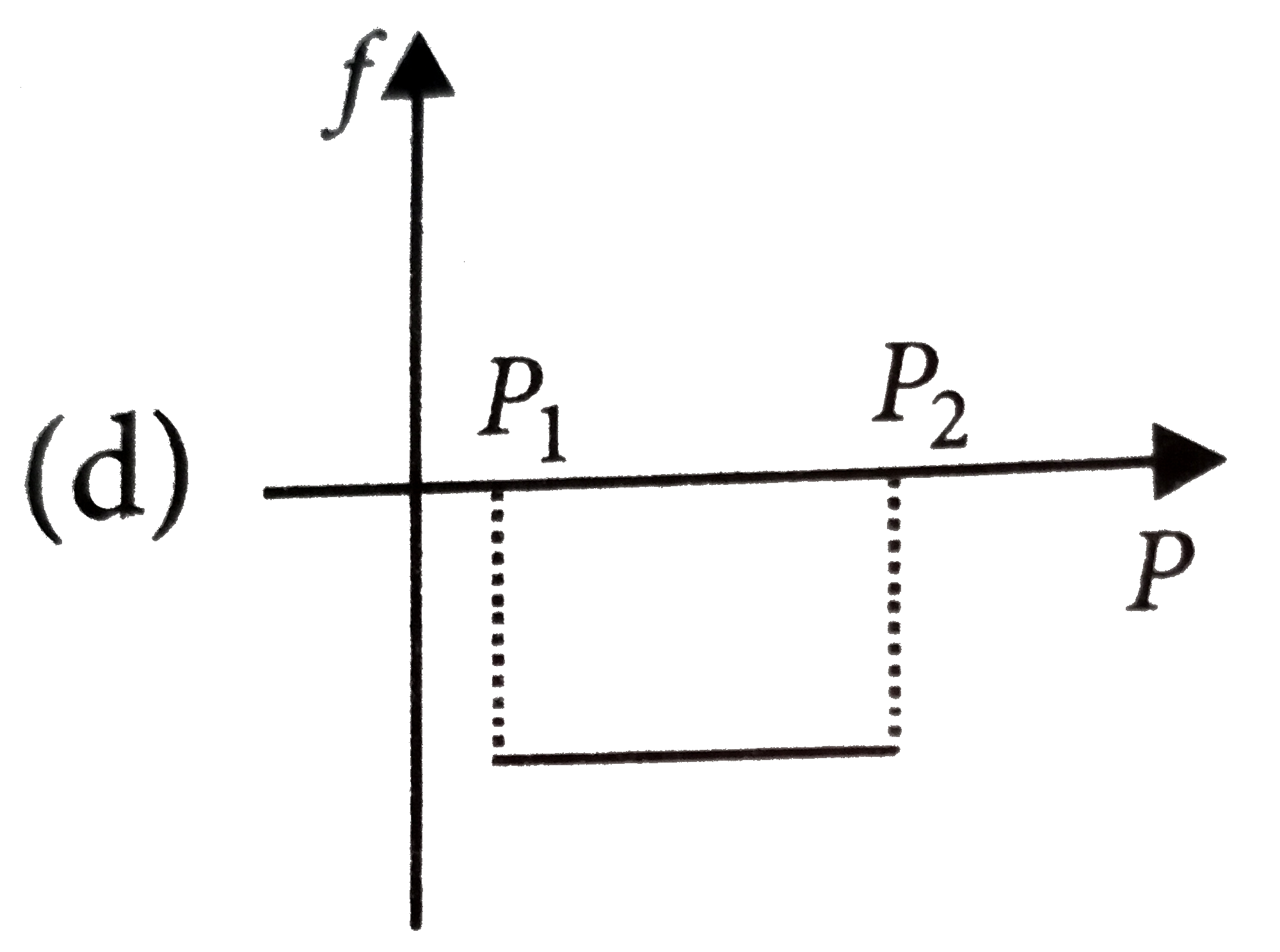
A block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
A10.3NB23.8NC11.9ND6.3N
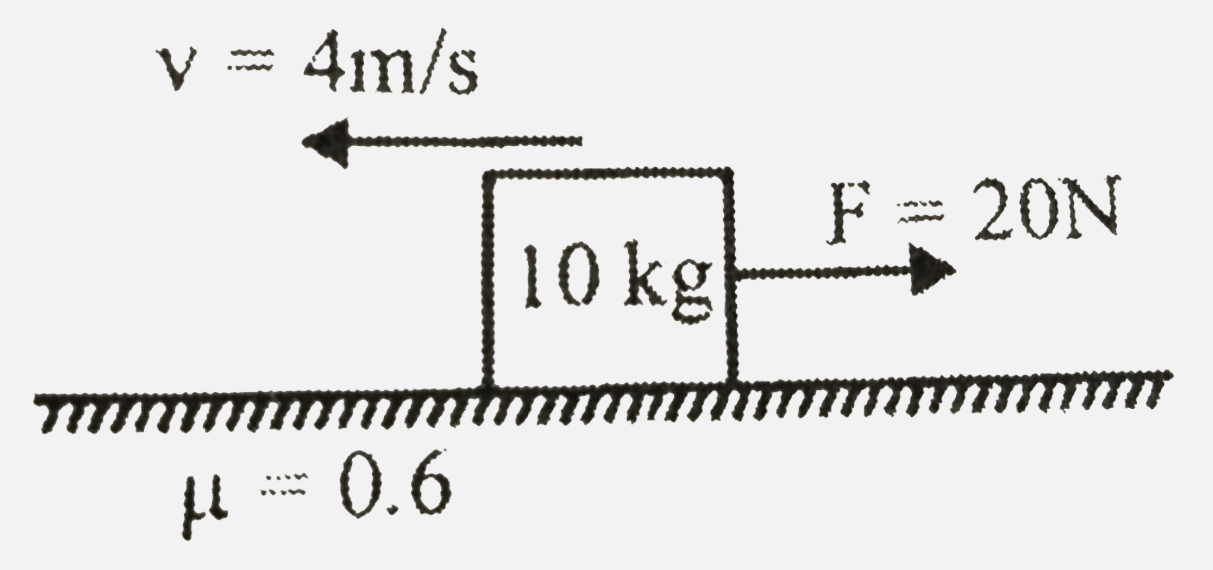
A block of mass 10 kg is moving on a rough surface as shown in figure. The frictional force acting on block is :-
View SolutionA block of mass M is kept on as rough horizontal surface. The coefficient of static frictionbetween the block and the surface is μ. The block is to be pulled by applying a force to it. What minimum force is needed to slide the block? In which direction should this force act?
View SolutionA block of mass m is lying on an inclined plane. The coefficient of friction between the plane and the block is μ. The force (F1) required to move the block up the inclined plane will be:-
View SolutionA block of mass 5 kg is at rest on a rough inclined surface. If angle of inclination of plane is 60∘, then force applied by it on block is
View SolutionA block of mass m is at rest on a rough inclined plane of angle of inclination θ. If coefficient of friction between the block and the inclined plane is μ, then the minimum value of force along the plane required to move the block on the plane is
View SolutionA block of mass 2kg rests on a rough inclined plane making an angle of 30∘ with the horizontal. The coefficient of static friction between the block and the plane is 0.7. The frictional force on the block is
View Solution

