Two plane mirrors are inclined at an angle of 60∘ with each other. An incident ray hits one of the mirror at an angle of 80∘ with the normal. Its angle of deviation after two reflections is
120∘
240∘
zero
60∘
The correct Answer is:A
To solve the problem of finding the angle of deviation after two reflections from two plane mirrors inclined at an angle of 60∘, we can follow these steps:
Step 1: Understand the setup
We have two plane mirrors inclined at an angle of 60∘. An incident ray strikes one of the mirrors at an angle of 80∘ with respect to the normal.
Step 2: Determine the angle of incidence
The angle of incidence i1 with respect to the normal is given as 80∘. Therefore, the angle of reflection r1 will also be 80∘ (according to the law of reflection).
Step 3: Calculate the angle of deviation after the first reflection
The angle of deviation D1 after the first reflection can be calculated using the formula:
D1=i1−r1+angle between mirrors
Here, the angle between the mirrors is 60∘. Thus,
D1=80∘−80∘+60∘=60∘
Step 4: Determine the angle of incidence for the second mirror
After the first reflection, the ray will strike the second mirror. The angle of incidence i2 for the second mirror can be calculated as:
i2=180∘−(r1+angle between mirrors)=180∘−(80∘+60∘)=40∘
Step 5: Calculate the angle of reflection for the second mirror
According to the law of reflection, the angle of reflection r2 will also be 40∘.
Step 6: Calculate the angle of deviation after the second reflection
The angle of deviation D2 after the second reflection can be calculated as:
D2=i2−r2+angle between mirrors
Substituting the values:
D2=40∘−40∘+60∘=60∘
Step 7: Calculate the total angle of deviation
The total angle of deviation D after two reflections is the sum of the deviations from both reflections:
D=D1+D2=60∘+60∘=120∘
Final Answer
The angle of deviation after two reflections is 120∘.
---
We have two plane mirrors inclined at an angle of 60∘. An incident ray strikes one of the mirrors at an angle of 80∘ with respect to the normal.
The angle of incidence i1 with respect to the normal is given as 80∘. Therefore, the angle of reflection r1 will also be 80∘ (according to the law of reflection).
The angle of deviation D1 after the first reflection can be calculated using the formula:
D1=i1−r1+angle between mirrors
Here, the angle between the mirrors is 60∘. Thus,
D1=80∘−80∘+60∘=60∘
After the first reflection, the ray will strike the second mirror. The angle of incidence i2 for the second mirror can be calculated as:
i2=180∘−(r1+angle between mirrors)=180∘−(80∘+60∘)=40∘
According to the law of reflection, the angle of reflection r2 will also be 40∘.
The angle of deviation D2 after the second reflection can be calculated as:
D2=i2−r2+angle between mirrors
Substituting the values:
D2=40∘−40∘+60∘=60∘
The total angle of deviation D after two reflections is the sum of the deviations from both reflections:
D=D1+D2=60∘+60∘=120∘
The angle of deviation after two reflections is 120∘.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS)
15 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE I LEVEL -II (ADVANCED) MORETHAN CORRECT ANSWER TYPE QUESTIONS)
7 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
Two plane mirrors are making an angle of 60∘ to each other. A light ray falls on one of the mirrors. The light ray is incident parallel to angular bisector of mirrors. How many reflection does the light ray undergo?
View SolutionTwo vertical plane mirrors are inclined at an angle of 60∘ with each other. A ray of light travelling horizontally is reflected first from one mirror and then from the other. The resultant deviation is
View SolutionA ray of light is incident at an angle of 30∘ with the plane of a plane mirror. Find the angle of reflection.
View SolutionTwo plane mirrors are inclined at an angle of 60∘ as shown in Figure. A ray of light parallel to M1 strikes M2. At what angle will the ray finally emerge?

View SolutionTwo plane mirrors are inclined to each other at an angle 60∘ if a ray of light incident on first mirror parallel to the second mirror, it is reflected from the second mirror
View SolutionTwo plane mirrors are arranged at right angles to each other as shown in figure.A ray of light is incident on the horizontal mirror at an angle θ. For what value of θthe ray emerges parallel to the incoming ray after reflection from the vertical mirror ?
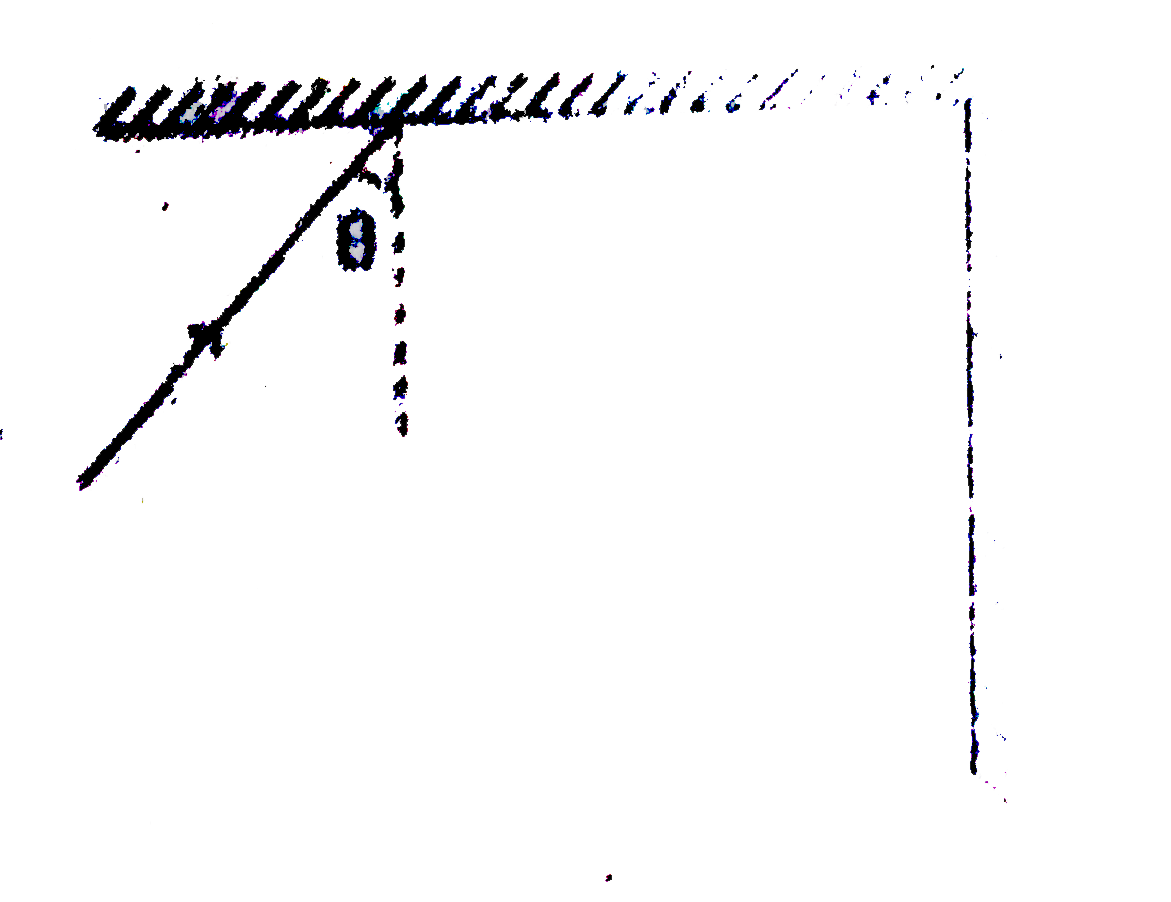
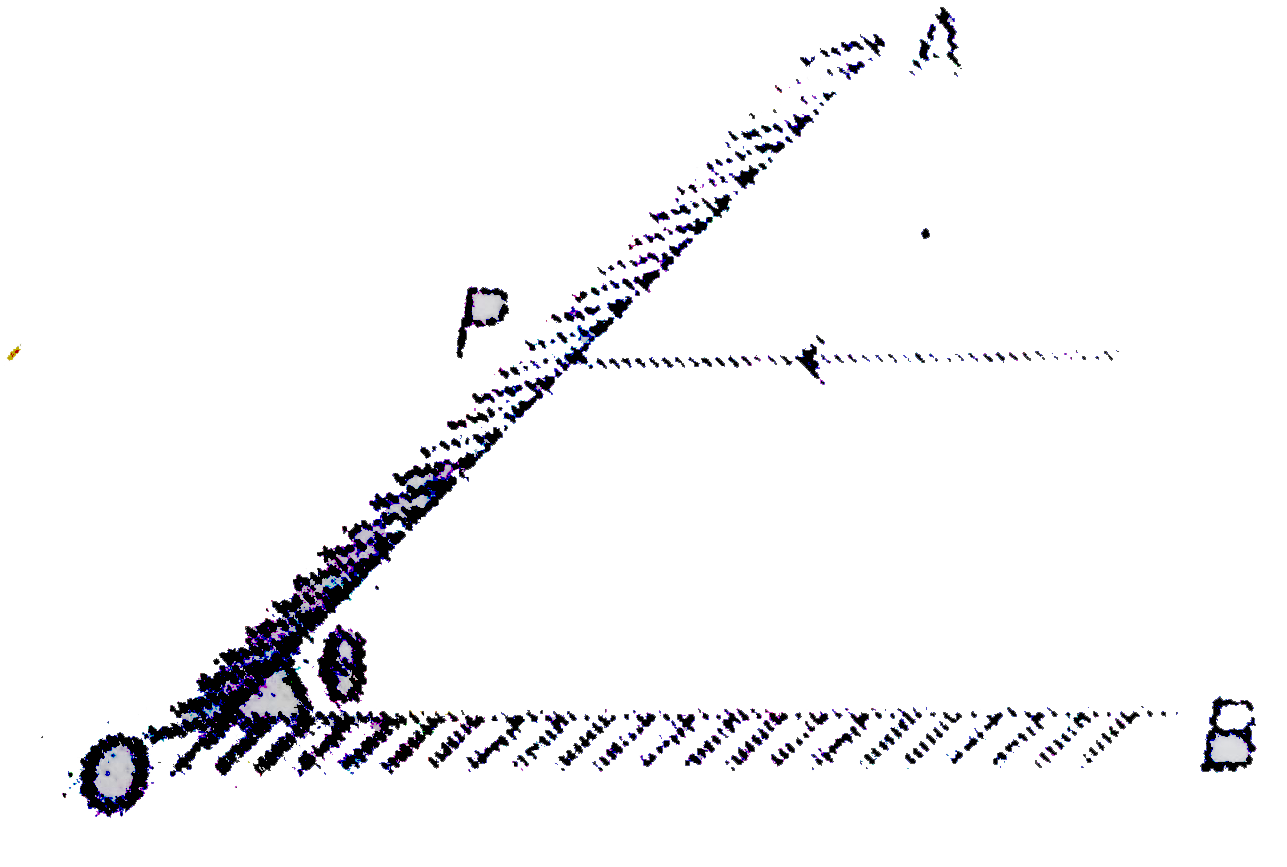
View SolutionTwo plane mirrors are inclined at angle θ as shown in figure. If a ray parallel to OB strikes the other mirror at P and finally emerges parallel to OA after two reflections then θ is equal to
View SolutionTwo plane mirrors are inclined to each other at an angle θ. A ray of light is reflected at one
mirror and then at the other. Find the total deviation of the ray.
View SolutionTwo plane mirror are inclined to each other at 90∘. A ray of light is incident on one mirror. The ray will undergo a total deviation of
View SolutionTwo plane mirrror are inclined to each other at 70∘. A ray of light is incident on one mirror. They ray after two reflections will undergo a total deviation of :
View Solution
