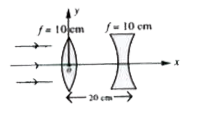
A convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure.

The co-ordinates of the image formed after refraction through both the lenses is
(15 cm, 0.25cm)
(10 cm+0.25cm)
(25cm, -0.5cm)
(15cm,+0.5cmC)
The correct Answer is:A
Step by step video & image solution for A convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure. The co-ordinates of the image formed after refraction through both the lenses is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) MATRIX MATCHING TYPE QUESTIONS)
1 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) INTEGER TYPE QUESTIONS)
2 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - LECTURE SHEET (EXERCISE III LEVEL -II (ADVAMCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
1 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
A convex lens of focal length 10 cm and a concave lens of same focal length in value are placed co-axially at a separation of 20 cm as shown in figure. A point object is at infinity on the principal axis. Take the optic center of convex lens as origin of co ordinate system and the principal axis as x-axis as shown in figure.
In the initial positin (as given in the passage ) if the concave lens has a velocit of 9 cm/s towards the convex lens, the velocity of the final image will be
View SolutionA convex lens of focal length A and a concave lens of focal length B are placed in contact. The focal length of the combination is
View SolutionA convex lens of focal length 40 cm is in contact with a concave lens of focal length 25 cm. The power of the combination is
View SolutionA convex lens of focal length 80 cm and a concave lens of focal length 50 cm are combined toghether. What will be their resulting power ?
View SolutionA convex lens of focal length 100 cm and a concave lens of focal length 10 cm are placed coaxialiy at a separation of 90 cm. If a parallel beam of light is incident on convex lens, then after passing through the two lenses the beam
View SolutionA convex lens of focal length 20cm and a convex mirror of focal length 10cm are placed co-axially 50cm apart from each other. An incident beam parallel to its principal axis is incideent on the convex lens. Locate the position of final image formed due to the combination.
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA convex lens A of focal length 20cm and a concave lens B of focal length 10 cm are kept along the same axis with a distance d between them. If a parallel beam, then d is
View SolutionA diverging lens of focal length 20 cm and a converging lens of focal length 30 cm are placed 15 cm apart with their principal axes coinciding. Where should an object be placed on the principal axis so that its image formed at infinity ?
View SolutionA convex lens of focal length 20cm and a concave lens of focal length f are mounted coaxially 5cm apart. Parallel beam of light incident on the convex lens emerges from the concave lens as a parallel beam. Then, f in cm is
View Solution
