Three diagrams are given each has equal radial of curvature of the curved surfaces. All the lenses have refractive index .

The ratio of focal lengths of P,Q,R is
The correct Answer is:A
Step by step video & image solution for Three diagrams are given each has equal radial of curvature of the curved surfaces. All the lenses have refractive index mu=1.5. The ratio of focal lengths of P,Q,R is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) INTEGER TYPE QUESTIONS)
4 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE -I (LEVEL-I(MAIN) STRAIGHT OBJECTIVE TYPE QUESTIONS)
21 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERCISE III LEVEL -II (ADVANCED) MORE THAN ONE CORRECT TYPE QUESTIONS)
2 Videos
- ELEMENTS OF VECTORSBOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
10 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
Similar Questions
The adjacent figure shows a thin plano-convex lens of refractive index μ1 and a thin plano-concave lens of refractive index μ2, both having same radius of curvature R of their curved surfaces. The thin lens of refractive index μ3 has radius of curvature R of both its surfaces. This lens is so placed in between the plano-convex and plano-concave lenses that the plane surfaces are parallel to each other.
The focal length of the combination is

View SolutionThe radius of curvature of the convex face of a plano convex lens is 12cm and the refractive index of the material of the lends 1.5. Then, the focal length of the lens is
View Solution
Knowledge Check
The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1D
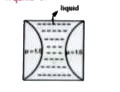
The effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
View SolutionGiven figures shows the arrangement of two lenses. The radii of curvature of all the curved surfaces are same. The ratio of the equivalent focal length of combinations P,Q and R is:

View SolutionFour combinations of two thin lenses are given in List I. The radius of curvature of all curved surfaces is r and the refractive index of all the lenses is 1.5 Match lens combinations in List I with their focal length in List II and select the correct answer using the code given below the lists.
(A) (p)2r
(B) (q)r2
( C) (r)−r
(D) (s)r.
Code :
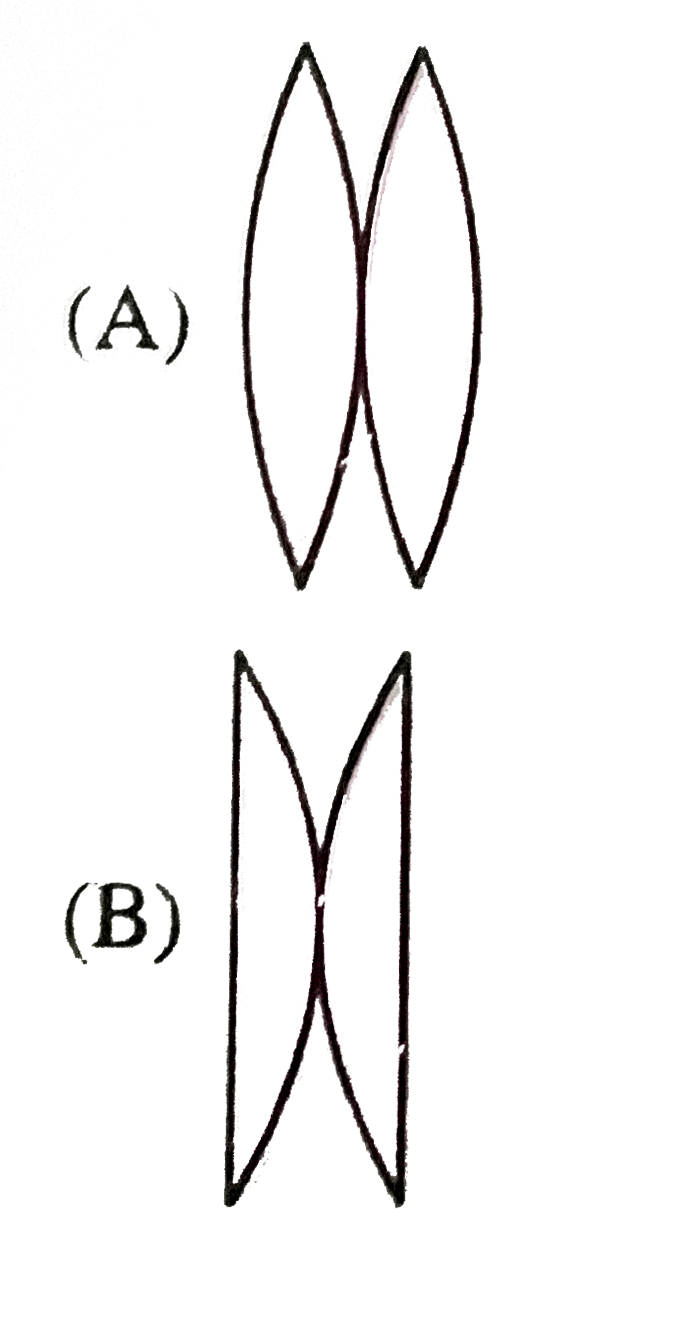
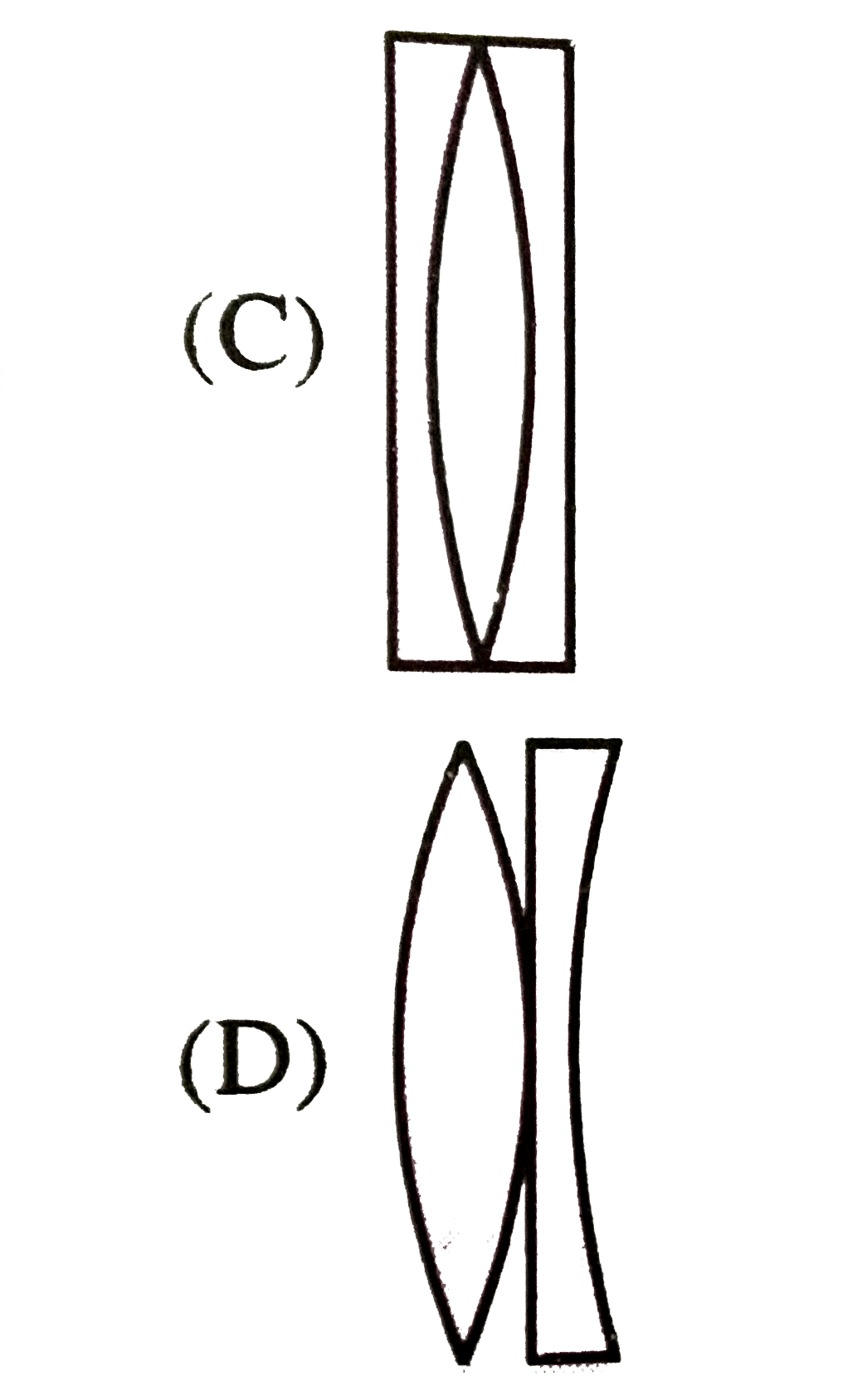
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionThe two surfaces of a biconvex lens has same radii of curvatures . This lens is made of glass of refractive index 1.5 and has a focal length of 10 cm in air. The lens is cut into two equal halves along a plane perpendicular to its principal axis to yield two plane - convex lenses. The two pieces are glued such that the convex surfaces touch each other. If this combination lens is immersed in water (refractive index =43 ), its focal length (in cm ) is
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View Solution
