The probability function of a random variable X is given by
p(x)=13, if x = -1, 0, 1
=0, otherwise.
Find the distribution function of X.
The correct Answer is:x−101P(X=x)1/31/31/3
To find the distribution function of the random variable X with the given probability function, we will follow these steps:
Step 1: Define the Probability Function
The probability function p(x) is defined as follows:
p(x)={13if x=−1,0,10otherwise
Step 2: Identify the Values of X
The random variable X can take the values:
- −1
- 0
- 1
Step 3: Calculate the Cumulative Distribution Function (CDF)
The cumulative distribution function F(x) is defined as:
F(x)=P(X≤x)
We will calculate F(x) for different intervals of x.
1. For x<−1:
F(x)=0(since P(X≤x)=0)
2. For −1≤x<0:
F(x)=P(X≤−1)=p(−1)=13
3. For 0≤x<1:
F(x)=P(X≤0)=P(X=−1)+P(X=0)=p(−1)+p(0)=13+13=23
4. For x≥1:
F(x)=P(X≤1)=P(X=−1)+P(X=0)+P(X=1)=p(−1)+p(0)+p(1)=13+13+13=1
Step 4: Summarize the CDF
Now we can summarize the cumulative distribution function F(x):
F(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩0if x<−113if −1≤x<023if 0≤x<11if x≥1
Final Answer
The distribution function F(x) of the random variable X is:
F(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩0if x<−113if −1≤x<023if 0≤x<11if x≥1
The probability function p(x) is defined as follows:
p(x)={13if x=−1,0,10otherwise
The random variable X can take the values:
- −1
- 0
- 1
The cumulative distribution function F(x) is defined as:
F(x)=P(X≤x)
We will calculate F(x) for different intervals of x.
F(x)=0(since P(X≤x)=0)
F(x)=P(X≤−1)=p(−1)=13
F(x)=P(X≤0)=P(X=−1)+P(X=0)=p(−1)+p(0)=13+13=23
F(x)=P(X≤1)=P(X=−1)+P(X=0)+P(X=1)=p(−1)+p(0)+p(1)=13+13+13=1
Now we can summarize the cumulative distribution function F(x):
F(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩0if x<−113if −1≤x<023if 0≤x<11if x≥1
The distribution function F(x) of the random variable X is:
F(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩0if x<−113if −1≤x<023if 0≤x<11if x≥1
Similar Questions
Consider the probability distribution of a random variable X.

V(X2)
View SolutionThe probability distribution of a random variable X is given as under:

Find k , and P (X<6) .
View SolutionThe probability of a random variable X is given below
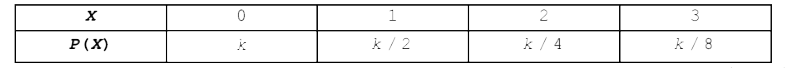
Find P(X≤2)+P(X>2)
View SolutionThe probability distribution of a discrete random variable X is given below
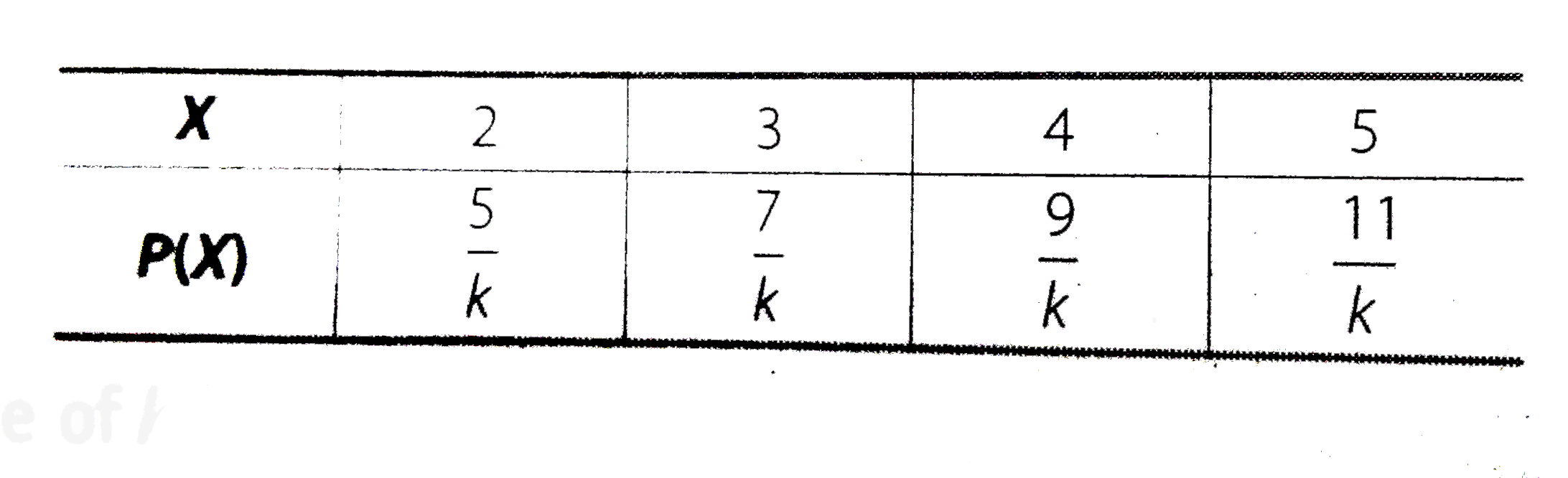
The value of k is
View SolutionThe probability distribution of a random variable X is given below.

Find k, mean and variance of X
View SolutionFind the value of k for probability distribution of a random variable X is give by:

View SolutionProbability distribhution of a random variable X is given by:

Find k, hence find the mean and variance of the distributions.
View SolutionThe probability of a random variable X is given below

Determine P(X≤2) and P(X>2)
View SolutionThe probability distribution of a discrate random variable X is given below :
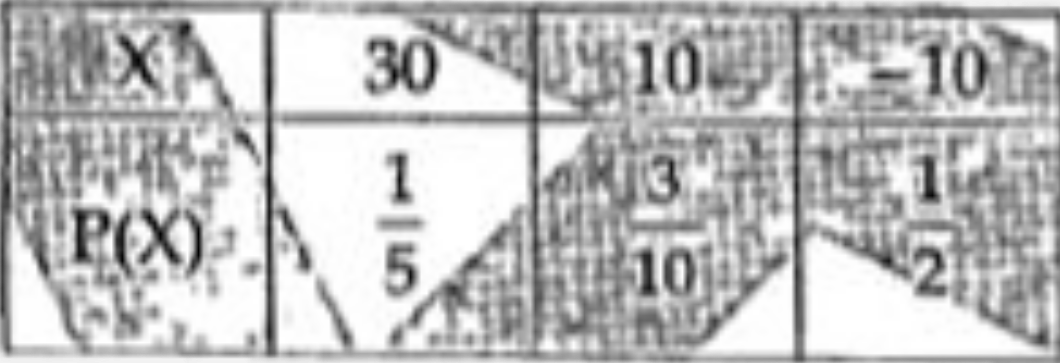
Then E(X) is equal to
View SolutionThe probability distribution of a discreate random variable X is given below :

The value of k is
View Solution
