If for a poisson distribution P(X=0)=0.2 then the variance of the distribution is
2
1
e
log5
The correct Answer is:D
To solve the problem, we need to find the variance of a Poisson distribution given that P(X=0)=0.2.
1. Understand the Poisson Distribution:
The probability mass function for a Poisson distribution is given by:
P(X=n)=e−λλnn!
where λ is the mean and variance of the distribution.
2. Set Up the Equation for P(X=0):
We know that P(X=0)=0.2. Using the formula for P(X=n) with n=0:
P(X=0)=e−λλ00!=e−λ
Therefore, we can set up the equation:
e−λ=0.2
3. Solve for λ:
To find λ, we take the natural logarithm of both sides:
−λ=ln(0.2)
Thus,
λ=−ln(0.2)
4. Simplify λ:
We can rewrite ln(0.2):
ln(0.2)=ln(15)=−ln(5)
Therefore,
λ=ln(5)
5. Determine the Variance:
In a Poisson distribution, the variance is equal to the mean, which is λ. Thus, the variance of the distribution is:
Variance=λ=ln(5)
Final Answer:
The variance of the Poisson distribution is ln(5).
---
The probability mass function for a Poisson distribution is given by:
P(X=n)=e−λλnn!
where λ is the mean and variance of the distribution.
We know that P(X=0)=0.2. Using the formula for P(X=n) with n=0:
P(X=0)=e−λλ00!=e−λ
Therefore, we can set up the equation:
e−λ=0.2
To find λ, we take the natural logarithm of both sides:
−λ=ln(0.2)
Thus,
λ=−ln(0.2)
We can rewrite ln(0.2):
ln(0.2)=ln(15)=−ln(5)
Therefore,
λ=ln(5)
In a Poisson distribution, the variance is equal to the mean, which is λ. Thus, the variance of the distribution is:
Variance=λ=ln(5)
The variance of the Poisson distribution is ln(5).
Similar Questions
Compute the variance of X whose distribution is given by
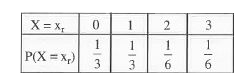
View SolutionIn a Poisson distribution if P(X=0)=P(X=1)=k, the value of k is
View SolutionA random variable X has the distribution.
Then , variance of the distribution, is
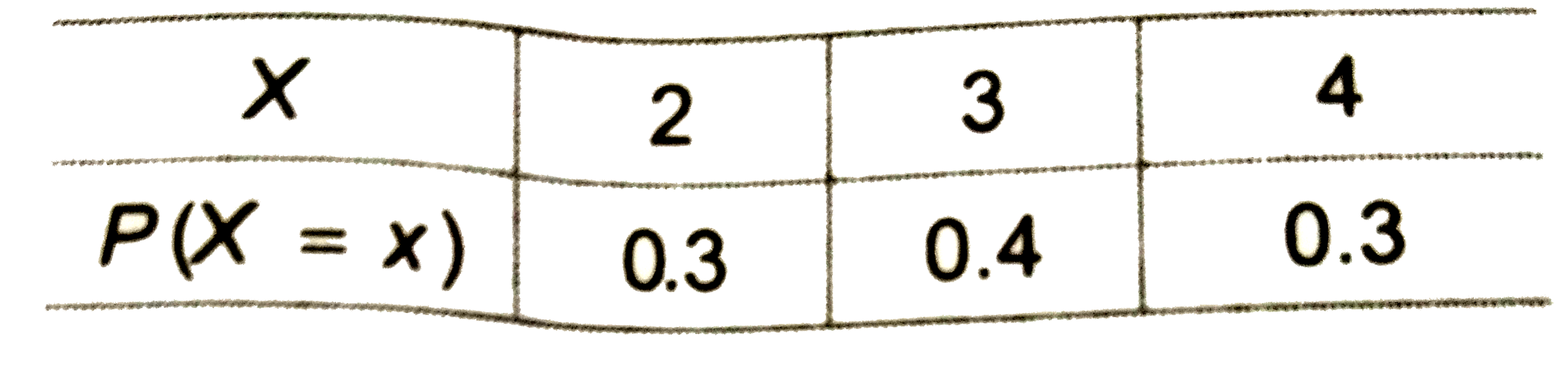
View SolutionIn a Poisson distribution P(X=0) =2P(X=1) then the standard deviation =
View SolutionIn a binomial distribution , prove that
mean > variance
View SolutionIf for a binomial distribution, the mean is 10 and the variance is 5, then find the parameters and P(X>6).
View SolutionIn a poisson distribution, the variance is m. The sum of terms in odd places in the distribution is
View SolutionIf X is a random variable with the following probability distribution
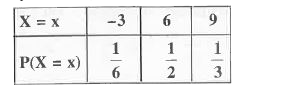
then the variance of X is
View SolutionFor a binomial distribution with mean 6 and variance 2, find the first two terms of the distribution.
View SolutionA : If the difference between the mean and variance of a binomial distribution for 5 trials is 5/9 then the distribution o is (2/3+1/3)5
R : The binomial distribution with parameters n, p is (q+p)n
View Solution
