If the number of telephone calls an operator receives between 10:00 am to 10:10 pm follow poisson distribution with mean 3. The probability that the operator receives one call during that interval the next day is
The correct Answer is:D
To solve the problem, we need to find the probability that an operator receives one telephone call between 10:00 am and 10:10 pm, given that the number of calls follows a Poisson distribution with a mean (λ) of 3.
1. Identify the Poisson Distribution Formula:
The probability of a Poisson random variable X taking a value x is given by the formula:
P(X=x)=λxe−λx!
where:
- λ is the mean number of occurrences (in this case, 3).
- x is the number of occurrences we want to find the probability for (in this case, 1).
2. Set the Values:
From the problem, we have:
- λ=3
- x=1
3. Substitute the Values into the Formula:
Now we substitute λ and x into the Poisson formula:
P(X=1)=31e−31!
4. Calculate Each Component:
- Calculate 31=3.
- Calculate 1!=1.
- The exponential term e−3 remains as is.
5. Combine the Results:
Now, substituting these values back into the equation gives:
P(X=1)=3⋅e−31=3⋅e−3
6. Final Result:
Thus, the probability that the operator receives one call during that interval is:
P(X=1)=3e−3
Conclusion:
The correct answer is 3e−3.
The probability of a Poisson random variable X taking a value x is given by the formula:
P(X=x)=λxe−λx!
where:
- λ is the mean number of occurrences (in this case, 3).
- x is the number of occurrences we want to find the probability for (in this case, 1).
From the problem, we have:
- λ=3
- x=1
Now we substitute λ and x into the Poisson formula:
P(X=1)=31e−31!
- Calculate 31=3.
- Calculate 1!=1.
- The exponential term e−3 remains as is.
Now, substituting these values back into the equation gives:
P(X=1)=3⋅e−31=3⋅e−3
Thus, the probability that the operator receives one call during that interval is:
P(X=1)=3e−3
The correct answer is 3e−3.
Similar Questions
In a telephone enquiry system, the number of phone calls regarding relevant enquiry follow poisson distribution with an average of five phone calls during 10-minute time intervals. The probability that there is at the most one phone call during a 10-minute time period is
View Solution10 mangoes are to be distributed among 5 persons. The probability that at least one of them will receive none, is
View SolutionSuppose that the number of telephone calls coming into a telephone exchange between 10 A.M. and 11 A.M., say, X1 is a random variable with possion distribution with parameter 2. Similarly the number of calls arriving between 11 A.M. and 12 noon, say X2 also follows a poisson distribution with parameter 6. If X1 and X2 are independent, what is the probability that more than 5 calls come in between 10 A.M. and 12 noon.
View SolutionWhat is the probability that a radioactive atom having a mean life of 10 days decays during the fifth day?
View SolutionIn a city 10 accident take place in a span of 50 days. Assuming that the number of accidents follow the Poisson distribution, the probability that three or more accident occure in a day , is
View Solution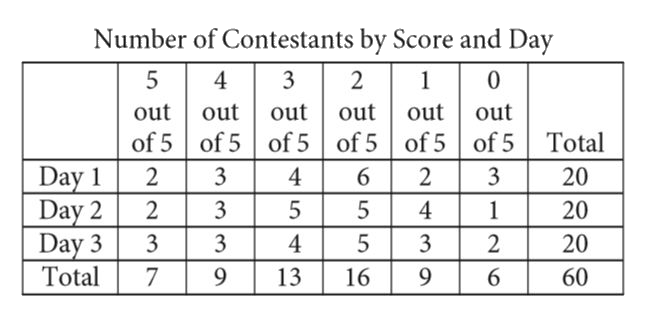
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?
View SolutionAssume that on a n average on telephone number out of 15 called between 2 P.M. and 3 P.M. on week days s busy. What is the probability that if six random selected telephone numbers are calld, at least 3 of them will be?
View Solution10 different books and 2 different pens are given to 3 boys so that each gets equal number of things. The probability that the same boy does not receive both the pens is
View SolutionA box contains 10 tickets numbered from 1 to 10 . Two tickets are drawn one by one without replacement. The probability that the "difference between the first drawn ticket number and the second is not less than 4" is
View Solution10 different books and 2 different pens are given to 3 boys so that each gets equal number of things. The probability that the some boy does not receive both the pens, is
View Solution
