In a binomial distribution the mean is 12 and the standard deviation is √3. Then the distribution is
(14+34)16
(14+14)16
(12+14)16
(34−14)16
The correct Answer is:A
To solve the problem, we need to find the parameters of the binomial distribution given the mean and standard deviation. Let's break it down step by step.
Step 1: Understand the Mean and Standard Deviation of a Binomial Distribution
The mean (μ) of a binomial distribution is given by the formula:
μ=n⋅p
where n is the number of trials and p is the probability of success.
The standard deviation (σ) is given by:
σ=√n⋅p⋅q
where q=1−p is the probability of failure.
Step 2: Set Up the Equations
From the problem, we know:
μ=12andσ=√3
This gives us two equations:
1. n⋅p=12 (1)
2. n⋅p⋅q=3 (since σ2=3) (2)
Step 3: Express q in Terms of p
From equation (1), we can express q in terms of p:
q=1−p
Step 4: Substitute q into the Standard Deviation Equation
Substituting q into equation (2):
n⋅p⋅(1−p)=3
Now substitute n⋅p=12 from equation (1):
12⋅(1−p)=3
Step 5: Solve for p
Now, solve for p:
12−12p=3
12p=12−3
12p=9
p=912=34
Step 6: Find q
Now that we have p, we can find q:
q=1−p=1−34=14
Step 7: Find n
Now, substitute p back into equation (1) to find n:
n⋅34=12
n=12⋅43=16
Step 8: Write the Binomial Distribution
Now we have:
- n=16
- p=34
- q=14
The binomial distribution can be expressed as:
B(n,p)=B(16,34)
Final Answer
Thus, the required binomial distribution is:
B(16,34)
---
The mean (μ) of a binomial distribution is given by the formula:
μ=n⋅p
where n is the number of trials and p is the probability of success.
σ=√n⋅p⋅q
where q=1−p is the probability of failure.
From the problem, we know:
μ=12andσ=√3
This gives us two equations:
1. n⋅p=12 (1)
2. n⋅p⋅q=3 (since σ2=3) (2)
From equation (1), we can express q in terms of p:
q=1−p
Substituting q into equation (2):
n⋅p⋅(1−p)=3
Now substitute n⋅p=12 from equation (1):
12⋅(1−p)=3
Now, solve for p:
12−12p=3
12p=12−3
12p=9
p=912=34
Now that we have p, we can find q:
q=1−p=1−34=14
Now, substitute p back into equation (1) to find n:
n⋅34=12
n=12⋅43=16
Now we have:
- n=16
- p=34
- q=14
B(n,p)=B(16,34)
Thus, the required binomial distribution is:
B(16,34)
Similar Questions
In a binomial distribution the mean is 20, standard deviation is √15 and p =
View SolutionIf for a binomial distribution the mean is 6 and the standard deviation is √2, then P(X=r)=
View SolutionIn a binomial distribution n=400, p=1/5, It's standard deviation is
View SolutionIn binomial probability distribution, mean is 3 and standard deviation is 32. Then the value of p is
View SolutionDetermine the binomial distribution whose mean is 9 and whose standard deviation is 32
View SolutionIf the mean of a binomial distribution is 20 and its standard deviation is 4, find p .
View SolutionFind the standard deviation of the following distribution :
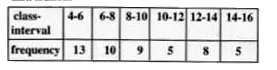
View SolutionIn a binomial distribution, n=5, the sum of the mean and variance is 1.8 . Then the distribution is
View SolutionDetermine the binomial distribution where means 9 and standard deviation is 32. Also, find the probability of obtainning at most one success.
View SolutionIn a binomial distribution , prove that
mean > variance
View Solution
