Find the sum and product of roots of x2+7x+12=0
The correct Answer is:-7, 12
To find the sum and product of the roots of the quadratic equation x2+7x+12=0, we can follow these steps:
Step 1: Identify the coefficients
The standard form of a quadratic equation is ax2+bx+c=0. Here, we have:
- a=1
- b=7
- c=12
Step 2: Use the formulas for sum and product of roots
For a quadratic equation ax2+bx+c=0:
- The sum of the roots α+β=−ba
- The product of the roots αβ=ca
Step 3: Calculate the sum of the roots
Using the formula for the sum of the roots:
α+β=−ba=−71=−7
Step 4: Calculate the product of the roots
Using the formula for the product of the roots:
αβ=ca=121=12
Conclusion
Thus, the sum of the roots is −7 and the product of the roots is 12.
Summary
- Sum of roots: −7
- Product of roots: 12
---
The standard form of a quadratic equation is ax2+bx+c=0. Here, we have:
- a=1
- b=7
- c=12
For a quadratic equation ax2+bx+c=0:
- The sum of the roots α+β=−ba
- The product of the roots αβ=ca
Using the formula for the sum of the roots:
α+β=−ba=−71=−7
Using the formula for the product of the roots:
αβ=ca=121=12
Thus, the sum of the roots is −7 and the product of the roots is 12.
- Sum of roots: −7
- Product of roots: 12
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following is a root of the equation x2−7x+12=0 ?
A5B−1C3D−4
Find the roots of 3x2−5x−12=0.
View SolutionAssertion (A ) : the number of roots of x4+2x3−7x2−8x+12=0
Reason (R ) : Every algebraic equation of degree n has n roots and nomore .View SolutionFind the equation whose roots are greater by 2 of the roots of x2−7x+12=0
View SolutionFind the equation whose roots are the squares of the roots of
x3+3x2−7x+6=0View SolutionConsider the graph of y = f(x) as shown in the following figure.
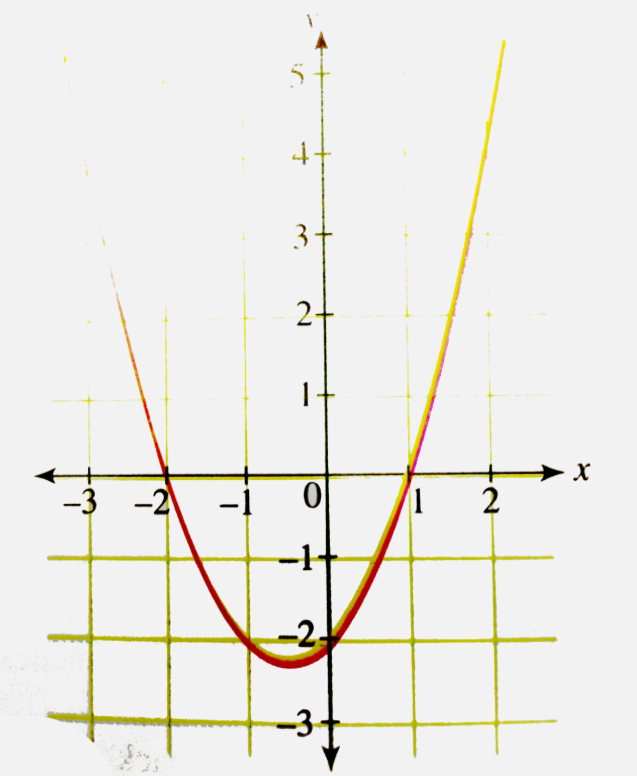
(i) Find the sum of the roots of the equation f (x) = 0.
(ii) Find the product of the roots of the equation f(x) = 4.
(iii) Find the absolute value of the difference of the roots of the equation f(x) = x+2 .View SolutionIf the product of the roots of
4x3+16x2−9x−a=0 is 9 , then find a .View SolutionFill in the blanks. If the product of the roots of the equation x2−3kx+2e2logk−1=0 is 7, then the roots are real for____________.
View Solution

