Given the following frequency distribution with some missing frequencies
Wages
No. of labourers
If the total frequency is 43 and median is 46.75 then the missing frequencies are
18,5
20,3
17,6
15,8
The correct Answer is:B
To find the missing frequencies f1 and f2 in the given frequency distribution, we will follow these steps:
Step 1: Set up the equation for total frequency
The total frequency is given as 43. The frequencies for the wage intervals are:
- 60-70: 5
- 50-60: 10
- 40-50: f1
- 30-40: 5
- 20-30: f2
We can write the equation for total frequency:
5+10+f1+5+f2=43
This simplifies to:
f1+f2+20=43
Thus,
f1+f2=23(Equation 1)
Step 2: Determine the median class
The median is given as 46.75. To find the median class, we need to find the cumulative frequency. The cumulative frequencies are:
- For 60-70: 5
- For 50-60: 15 (5 + 10)
- For 40-50: 15+f1
- For 30-40: 20+f1
- For 20-30: 20+f1+f2
Since the median is 46.75, it falls in the class 40-50, as the cumulative frequency just before this class is 15.
Step 3: Use the median formula
The median formula is:
Median=L+(n2−CF)⋅hf
Where:
- L = lower limit of the median class = 40
- n = total frequency = 43
- CF = cumulative frequency of the class before the median class = 15
- h = class width = 10 (from 40 to 50)
- f = frequency of the median class = f1
Substituting the values into the formula:
46.75=40+(432−15)⋅10f1
Calculating 432:
432=21.5
Thus,
46.75=40+(21.5−15)⋅10f1
This simplifies to:
46.75=40+6.5⋅10f1
Subtracting 40 from both sides:
6.75=6.5⋅10f1
Rearranging gives:
f1=6.5⋅106.75
Calculating this:
f1=656.75≈9.63
Step 4: Substitute f1 back to find f2
Now we substitute f1 back into Equation 1:
f2=23−f1
Substituting the value of f1:
f2=23−9.63≈13.37
Conclusion
The missing frequencies are approximately:
f1≈20andf2≈3
The total frequency is given as 43. The frequencies for the wage intervals are:
- 60-70: 5
- 50-60: 10
- 40-50: f1
- 30-40: 5
- 20-30: f2
5+10+f1+5+f2=43
This simplifies to:
f1+f2+20=43
Thus,
f1+f2=23(Equation 1)
The median is given as 46.75. To find the median class, we need to find the cumulative frequency. The cumulative frequencies are:
- For 60-70: 5
- For 50-60: 15 (5 + 10)
- For 40-50: 15+f1
- For 30-40: 20+f1
- For 20-30: 20+f1+f2
The median formula is:
Median=L+(n2−CF)⋅hf
Where:
- L = lower limit of the median class = 40
- n = total frequency = 43
- CF = cumulative frequency of the class before the median class = 15
- h = class width = 10 (from 40 to 50)
- f = frequency of the median class = f1
46.75=40+(432−15)⋅10f1
Calculating 432:
432=21.5
Thus,
46.75=40+(21.5−15)⋅10f1
This simplifies to:
46.75=40+6.5⋅10f1
Subtracting 40 from both sides:
6.75=6.5⋅10f1
Rearranging gives:
f1=6.5⋅106.75
Calculating this:
f1=656.75≈9.63
Now we substitute f1 back into Equation 1:
f2=23−f1
Substituting the value of f1:
f2=23−9.63≈13.37
The missing frequencies are approximately:
f1≈20andf2≈3
Similar Questions
Given the following frequency distribution with some missing frequencies .
Class10−2020−3030−4040−5050−6060−7070−80 f 180 − 34 180 136 − 50
If the total frequency is 685 and median is 42.6 then the missing frequencies are
View SolutionIf the median of the following frequency distribution is 28.5 find the missing frequencies: Class interval: 0-10 10-20 20-30 30-40 40-50 50-60 Total Frequency: 5 f1 20 15 f2 5 60
View SolutionIf the median of the following frequency distribution is 46, find the missing frequencies. Variable: 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Total Frequency: 12 30 ? 65 ? 25 18 230
View SolutionThe mean of the following frequency distribution is 50. Find the value of p. Classes 0-20 20-40 40-60 60-80 80-100 Frequency 17 28 32 p 19
View SolutionThe mean of the following distribution is 52 and the frequency of class interval 30-40 is f. Find f.
View SolutionConsider the following distribution
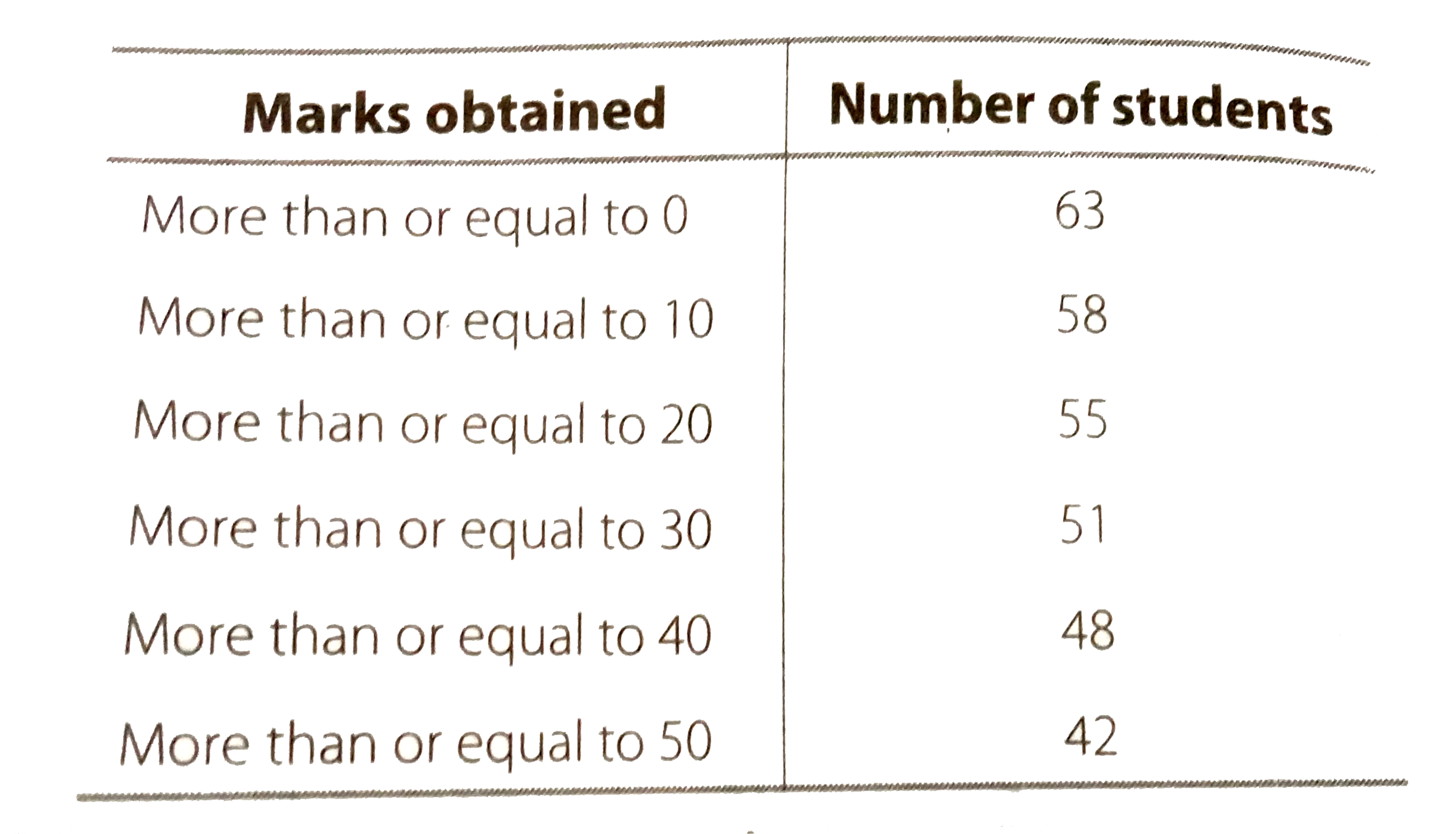
Frequency of the class 30-40 is
View SolutionFind the mean of the following frequency distribution using step-deviation method. Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 10 15 8 10
View SolutionFind the mean of the following frequency distribution, using step-deviation method: Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 12 13 10 8
View SolutionFind the mean of the following frequency distributions: Classinterval: 10−30 30−50 50−70 70−90 90−110 110−130 Frequency: 5 8 12 20 3 2
View SolutionFind the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View Solution