Observe the following statements
Statement - I : p∨~(p∧q) is a tautology
Statement - II : A statement pattern is called a tautology, if it is always true, whatever may be the true value of constitute statements.
Statement - I is true, Stateent - II is true, Statement - II is a correct explanation of Statement - I
Statement - I is true, Statement - II is true, Statement - II is not a correct explanation of Statement - I
statement 1 is true and statement 2 is false
statement 1 is false and statement 2 is true
To determine whether the statements provided are true, we will analyze each statement step by step.
Step 1: Define the Statements
- Statement I: p∨¬(p∧q) is a tautology.
- Statement II: A statement pattern is called a tautology if it is always true, regardless of the truth values of its constituent statements.
Step 2: Understand the Components
- The logical symbols used are:
- p: A propositional variable (can be true or false).
- q: Another propositional variable (can also be true or false).
- ∨: Logical OR.
- ∧: Logical AND.
- ¬: Logical NOT (negation).
Step 3: Create a Truth Table
We will create a truth table to evaluate p∨¬(p∧q).
| p | q | p∧q | ¬(p∧q) | p∨¬(p∧q) |
|---------|---------|------------------|-----------------------|-------------------------------|
| T | T | T | F | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | T | T |
Step 4: Analyze the Truth Table
- From the truth table, we can see that the final column p∨¬(p∧q) is always true (T) for all combinations of truth values of p and q.
- Therefore, Statement I is true: p∨¬(p∧q) is indeed a tautology.
Step 5: Evaluate Statement II
- Statement II defines what a tautology is: a statement that is always true regardless of the truth values of its components.
- Since we have established that Statement I is a tautology, Statement II correctly describes what a tautology is.
Conclusion
- Both Statement I and Statement II are true.
- Statement II is a correct explanation of Statement I.
Thus, the final answer is:
- Statement I is true.
- Statement II is true.
- Statement I: p∨¬(p∧q) is a tautology.
- Statement II: A statement pattern is called a tautology if it is always true, regardless of the truth values of its constituent statements.
- The logical symbols used are:
- p: A propositional variable (can be true or false).
- q: Another propositional variable (can also be true or false).
- ∨: Logical OR.
- ∧: Logical AND.
- ¬: Logical NOT (negation).
We will create a truth table to evaluate p∨¬(p∧q).
|---------|---------|------------------|-----------------------|-------------------------------|
| T | T | T | F | T |
| T | F | F | T | T |
| F | T | F | T | T |
| F | F | F | T | T |
- From the truth table, we can see that the final column p∨¬(p∧q) is always true (T) for all combinations of truth values of p and q.
- Therefore, Statement I is true: p∨¬(p∧q) is indeed a tautology.
- Statement II defines what a tautology is: a statement that is always true regardless of the truth values of its components.
- Since we have established that Statement I is a tautology, Statement II correctly describes what a tautology is.
- Both Statement I and Statement II are true.
- Statement II is a correct explanation of Statement I.
- Statement I is true.
- Statement II is true.
Similar Questions
Observe the following statements :
Statements - I : (p∨q)∧(~p∧~q) is a contradiction.
Statement - II : A statement pattern is called a contradiction, it it is a always false, whatever may the truth values of its consitutes statements.
View SolutionVerify that the statement P∨~(p∧q) is a tautology.
View SolutionWhich of the following statements is tautology ?
View SolutionObserve the following reaction and determine True statement
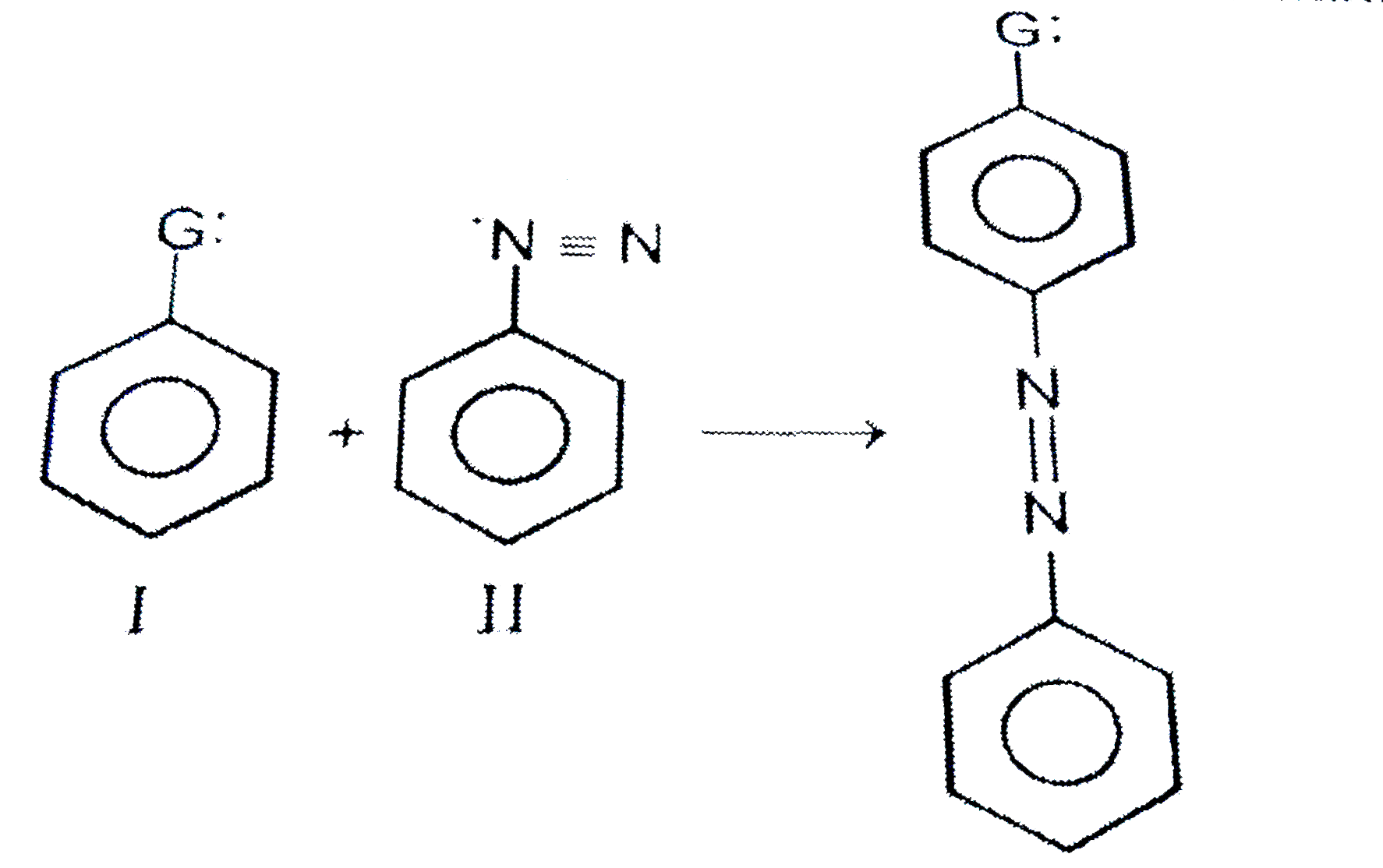
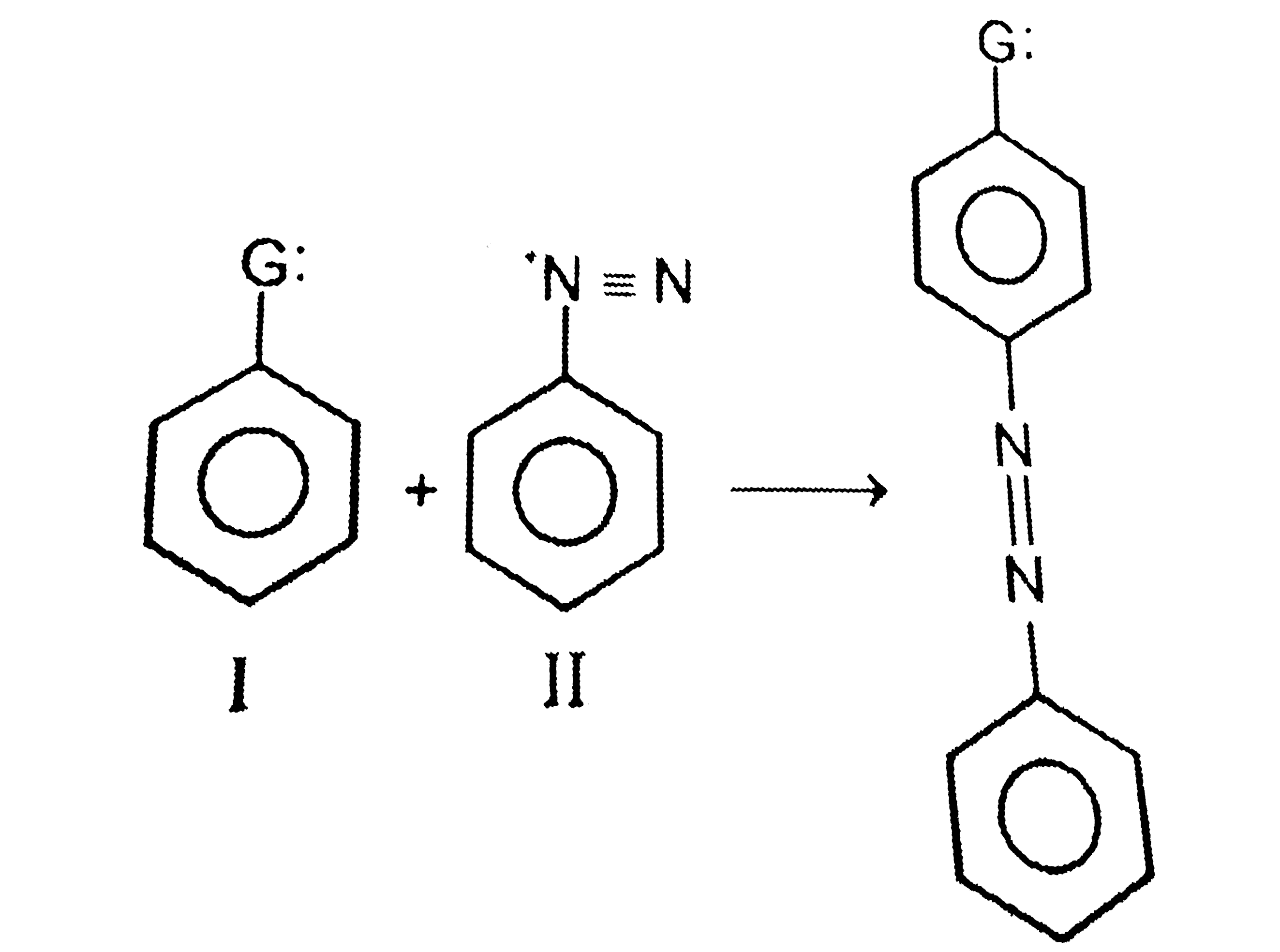
View SolutionObserve the following reaction and determine True statement
View SolutionWhich of the following statements is a tautology ?
View SolutionWhich of the following statement is a tautology?
View SolutionWhich of the following statement is a tautology?
View SolutionThe following statement (p→q)→[(~p→q)→q] is
View SolutionGiven the following two statements
S1:(p∧:p)→(p∧q) is a tautology.
S2:(p∨:p)→(p∨q) is a fallacy
View Solution
