The apparent weight of a freely falling body is
zero
increased
decreased
constant
The correct Answer is:A
To find the apparent weight of a freely falling body, we can follow these steps:
Step 1: Understand the Forces Acting on the Body
The body is in free fall, which means the only force acting on it is the gravitational force. The weight of the body can be expressed as:
W=mg
where m is the mass of the body and g is the acceleration due to gravity.
Step 2: Define Apparent Weight
The apparent weight is the normal force (reaction force) acting on the body. In a freely falling situation, the normal force is what we refer to as the apparent weight.
Step 3: Apply Newton's Second Law
According to Newton's second law, the net force acting on the body is equal to the mass of the body multiplied by its acceleration:
Fnet=ma
In this case, the net force is the difference between the gravitational force (weight) and the normal force:
Fnet=mg−R
where R is the normal force (apparent weight).
Step 4: Set the Acceleration
Since the body is freely falling, the acceleration a is equal to g:
a=g
Step 5: Substitute and Rearrange the Equation
Substituting a=g into the equation gives us:
mg−R=mg
Step 6: Solve for the Normal Force
Rearranging the equation to solve for R:
R=mg−mg
R=0
Conclusion
The apparent weight of a freely falling body is:
R=0
Thus, the answer is that the apparent weight of a freely falling body is 0.
---
The body is in free fall, which means the only force acting on it is the gravitational force. The weight of the body can be expressed as:
W=mg
where m is the mass of the body and g is the acceleration due to gravity.
The apparent weight is the normal force (reaction force) acting on the body. In a freely falling situation, the normal force is what we refer to as the apparent weight.
According to Newton's second law, the net force acting on the body is equal to the mass of the body multiplied by its acceleration:
Fnet=ma
Fnet=mg−R
where R is the normal force (apparent weight).
Since the body is freely falling, the acceleration a is equal to g:
a=g
Substituting a=g into the equation gives us:
mg−R=mg
Rearranging the equation to solve for R:
R=mg−mg
R=0
The apparent weight of a freely falling body is:
R=0
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE
106 Videos
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - Application
6 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
For a freely falling body
View SolutionThe apparent weight of a body
View SolutionA : The apparent weight of a body floating on the surface of a liquid is zero.
R : The net force on a body floating on the surface of a liquid is zero.
View Solution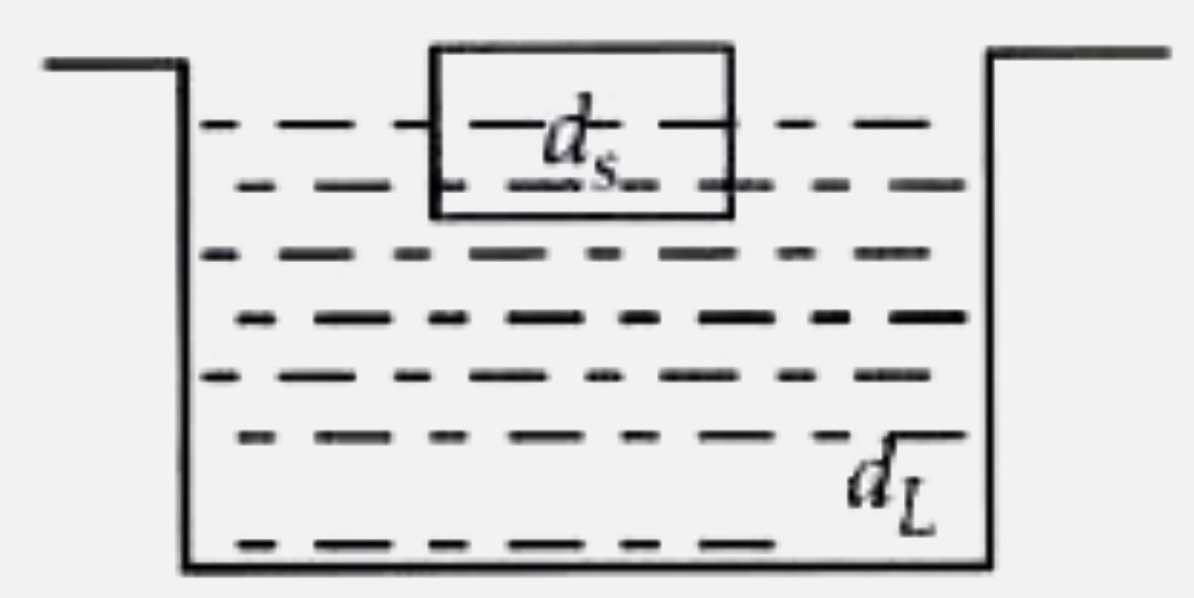
The figure above shows a solid of density dS floating in a liquid of density dL.
What is the apparent weight of the floating body?
View SolutionThe velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
View SolutionThe apparent weight of man inside a lift moving up with certain acceleration is 900N. When the lift is coming down with the same acceleration apparent weight is found to be 300N. The mass of the man is (g = 10ms−2)
View SolutionThe ratio of times taken by freely falling body to cover first metre, second metre,... is
View SolutionThe distance moved by a freely falling body (startibg from rest) during st,2nd,3nd,……nth second of its motion are propotional to .
View SolutionA man of weight mg is moving up in a rocket with acceleration 4 g . The apparent weight of the man in the rocket is
View SolutionThe weight of a body at the poles is greater than the weight at the equator. Is it the actual weight or the apparent weight we are talking about? Does your answer depend on whether only the earth's rotation is taken into account or the flattening of the earth at the poles is also taken into account?
View Solution
