A uniform rope of length L, resting on a frictionless horizontal table is pulled at one end by a force F. What is the tension in the rope at a distance x form the end where the force is applied?
F(L -x)
Fx/L
(L-x) / F
F(1- x/L)
The correct Answer is:D
To find the tension in a uniform rope of length L that is resting on a frictionless horizontal table and is pulled at one end by a force F, we can follow these steps:
Step 1: Understand the System
We have a uniform rope of length L on a frictionless table. A force F is applied at one end of the rope. We need to find the tension T at a distance x from the end where the force is applied.
Step 2: Define the Mass of the Rope
Let the total mass of the rope be m. The mass per unit length of the rope is given by:
mass per unit length=mL
Step 3: Determine the Mass of the Rope Segments
- The mass of the segment of the rope from the end where the force is applied to the point x is:
ma=mL⋅x
- The mass of the remaining segment of the rope from point x to the other end is:
mb=mL⋅(L−x)
Step 4: Apply Newton's Second Law
Assume the entire rope moves with an acceleration a when the force F is applied.
For the segment from the end to point x:
Using Newton's second law for this segment:
F−T=ma⋅a
Substituting ma:
F−T=(mL⋅x)a(Equation 1)
For the segment from point x to the end of the rope:
Using Newton's second law for this segment:
T=mb⋅a
Substituting mb:
T=(mL⋅(L−x))a(Equation 2)
Step 5: Solve for Acceleration a
Adding Equation 1 and Equation 2 gives:
F=ma⋅a+mb⋅a
Substituting the expressions for ma and mb:
F=(mL⋅x+mL⋅(L−x))a
This simplifies to:
F=mL⋅L⋅a=m⋅a
Thus, we can express acceleration as:
a=Fm
Step 6: Substitute a Back to Find Tension T
Now substitute a back into Equation 2:
T=(mL⋅(L−x))⋅Fm
The mass m cancels out:
T=FL⋅(L−x)
This can be rewritten as:
T=F⋅(1−xL)
Final Answer
The tension in the rope at a distance x from the end where the force is applied is:
T=F⋅(1−xL)
We have a uniform rope of length L on a frictionless table. A force F is applied at one end of the rope. We need to find the tension T at a distance x from the end where the force is applied.
Let the total mass of the rope be m. The mass per unit length of the rope is given by:
mass per unit length=mL
- The mass of the segment of the rope from the end where the force is applied to the point x is:
ma=mL⋅x
- The mass of the remaining segment of the rope from point x to the other end is:
mb=mL⋅(L−x)
Assume the entire rope moves with an acceleration a when the force F is applied.
Using Newton's second law for this segment:
F−T=ma⋅a
Substituting ma:
F−T=(mL⋅x)a(Equation 1)
Using Newton's second law for this segment:
T=mb⋅a
Substituting mb:
T=(mL⋅(L−x))a(Equation 2)
Adding Equation 1 and Equation 2 gives:
F=ma⋅a+mb⋅a
Substituting the expressions for ma and mb:
F=(mL⋅x+mL⋅(L−x))a
This simplifies to:
F=mL⋅L⋅a=m⋅a
Thus, we can express acceleration as:
a=Fm
Now substitute a back into Equation 2:
T=(mL⋅(L−x))⋅Fm
The mass m cancels out:
T=FL⋅(L−x)
This can be rewritten as:
T=F⋅(1−xL)
The tension in the rope at a distance x from the end where the force is applied is:
T=F⋅(1−xL)
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE - II
136 Videos
- GEOMETRICAL OPTICSBOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL-II PRACTICE SHEET (ADVANCED) INTEGER TYPE QUESTIONS)
10 Videos
- LOGIC GATESBOOK - AAKASH SERIESCHAPTER - LOGIC GATESEXERCISE - Exercise (Very Short Answer)
10 Videos
Similar Questions
A horizontal uniform rope of length L, resting on a frictionless horizontal surface, is pulled at one end by force F. What is the tension in the rope at a distance l from the end where the force is applied?
View SolutionA string of length L and mass M is lying on a horizontal table. A force F is applied at one of its ends. Tension in the string at a distance x from the end at which force is applied is
View Solution
Knowledge Check
A rope of length L is pulled by a constant force F. What is the tension in the rope at a distance x from the end where the force is applied ?
AFL/xBF(L−x)/LCFL/(L−x)DFx/(L−x)
A uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Acceleration (A) of the rope is
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Expression Tx of tension at a point at distance x from the end A is
View SolutionA uniform rope of length 5m is on a smooth horizontal surface. It is being pulled by a horizontal force of 20 N at one end. The ratio of tension at a distance of 2m from force end to tension at a distance of 2m from free end is,
View SolutionA uniform rope of mass (m) and length (L) placed on frictionless horizontal ground is being pulled by two forces FAandFB at its ends as shown in the figure. As a result, the rope accelerates toward the right.

Tension (T) at the mid point of the pore is
View SolutionA rope placed straight on a frictionless floor is pulled longitudinally by a force F. Tension force T developed in the rope at a point varies with distance x of the point from the rear end as shown in the graph. What can you certainly conclude about density of the rope?
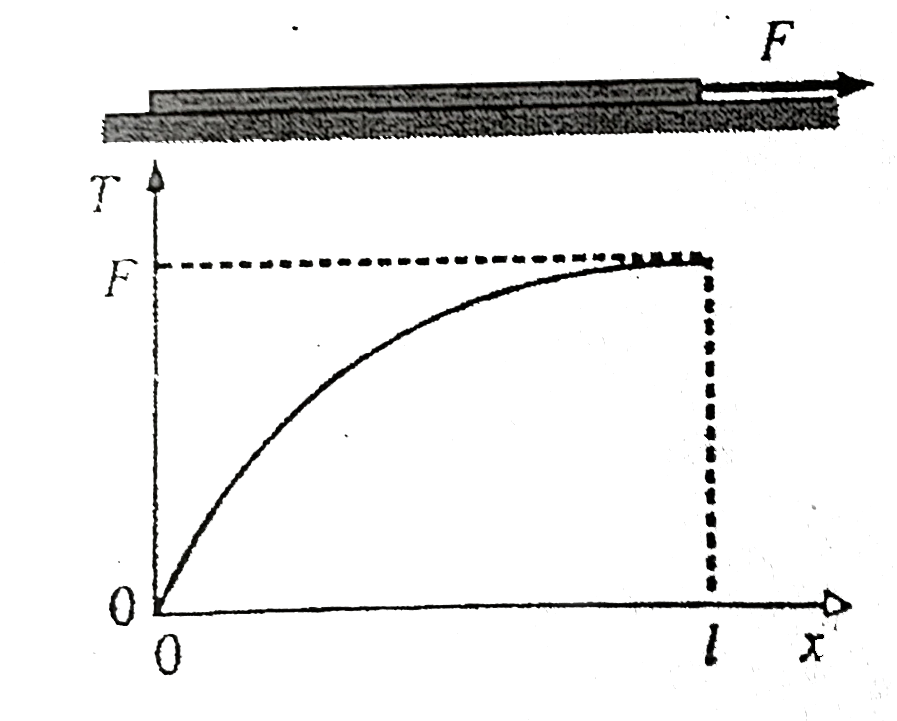
View SolutionA uniform rod of mass M and length L lies flat on a frictionless horizantal surface. Two forces F and 2F are applied along the length of the rod as shown. The tension in the rod at point P is

View SolutionA rope of length 10m and linear density 0.5kg/m is lying length wise on a smooth horizontal floor It is pulled by a force of 25N. The tension in the rope at a point 6m away from the point of application is .
View Solution
