Find the mean deviation of the set of of numbers 3, 10, 9, 4, 7, 9, 14 fromMean and Median and show that mean deviation from Mean is greater than that from Median
To find the mean deviation of the set of numbers 3,10,9,4,7,9,14 from both the mean and the median, and to show that the mean deviation from the mean is greater than that from the median, we will follow these steps:
Step 1: Calculate the Mean
The mean is calculated by summing all the numbers and dividing by the total count of numbers.
Mean=3+10+9+4+7+9+147
Calculating the sum:
3+10+9+4+7+9+14=56
Now, divide by the number of observations (7):
Mean=567=8
Step 2: Calculate the Mean Deviation from the Mean
The mean deviation from the mean is calculated using the formula:
Mean Deviation=∑|xi−Mean|n
Where xi are the data points and n is the number of observations.
Calculating the absolute deviations:
- |3−8|=5
- |10−8|=2
- |9−8|=1
- |4−8|=4
- |7−8|=1
- |9−8|=1
- |14−8|=6
Now, summing these absolute deviations:
5+2+1+4+1+1+6=20
Now, divide by the number of observations (7):
Mean Deviation from Mean=207≈2.857
Step 3: Calculate the Median
To find the median, we first arrange the numbers in ascending order:
3,4,7,9,9,10,14
Since there are 7 numbers (an odd count), the median is the middle number:
Median=9
Step 4: Calculate the Mean Deviation from the Median
Using the same formula for mean deviation:
Mean Deviation from Median=∑|xi−Median|n
Calculating the absolute deviations from the median:
- |3−9|=6
- |4−9|=5
- |7−9|=2
- |9−9|=0
- |9−9|=0
- |10−9|=1
- |14−9|=5
Now, summing these absolute deviations:
6+5+2+0+0+1+5=19
Now, divide by the number of observations (7):
Mean Deviation from Median=197≈2.714
Step 5: Compare the Mean Deviations
Now we compare the two mean deviations:
- Mean Deviation from Mean: ≈2.857
- Mean Deviation from Median: ≈2.714
Thus, we can conclude that:
Mean Deviation from Mean>Mean Deviation from Median
Final Result
The mean deviation from the mean is approximately 2.857 and from the median is approximately 2.714. Therefore, it is shown that the mean deviation from the mean is greater than that from the median.
---
The mean is calculated by summing all the numbers and dividing by the total count of numbers.
The mean deviation from the mean is calculated using the formula:
- |10−8|=2
- |9−8|=1
- |4−8|=4
- |7−8|=1
- |9−8|=1
- |14−8|=6
To find the median, we first arrange the numbers in ascending order:
Using the same formula for mean deviation:
- |4−9|=5
- |7−9|=2
- |9−9|=0
- |9−9|=0
- |10−9|=1
- |14−9|=5
Now we compare the two mean deviations:
- Mean Deviation from Median: ≈2.714
The mean deviation from the mean is approximately 2.857 and from the median is approximately 2.714. Therefore, it is shown that the mean deviation from the mean is greater than that from the median.
Similar Questions
Find the mean deviation from the mean of observations -1, 0, 4 ?
View SolutionThe mean deviation of the number 3, 4, 5, 6, 7 from median is
View SolutionFind the mean deviation using median:
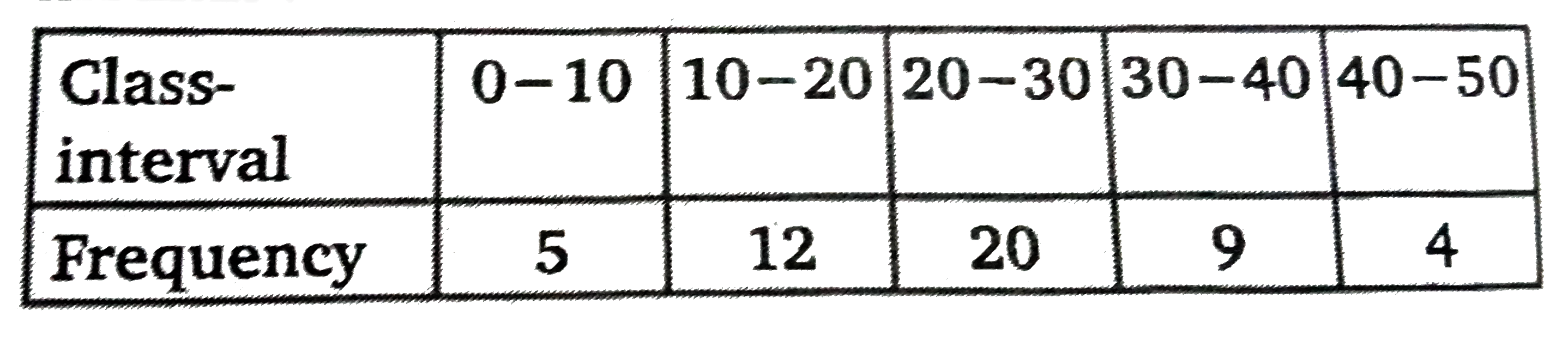
View SolutionFind the sum of the deviations of the variate values 3, 4, 6, 8, 14 from their mean.
View SolutionFind the mean deviation from the mean for the set of obervations 1,2,3.
View SolutionFind the mean deviation of the first three odd natural numbers from their mean.
View SolutionFind the mean of the following set of numbers:
6,9,11,12 and 7
View SolutionMean deviation from mean of the data is

View SolutionMean deviation from the mean for data 6, 7 10, 12, 13, 4, 8, 12 is
View SolutionFind the sum of the deviations of the variate values 3,4,6,8, 14 from their mean.
View Solution
