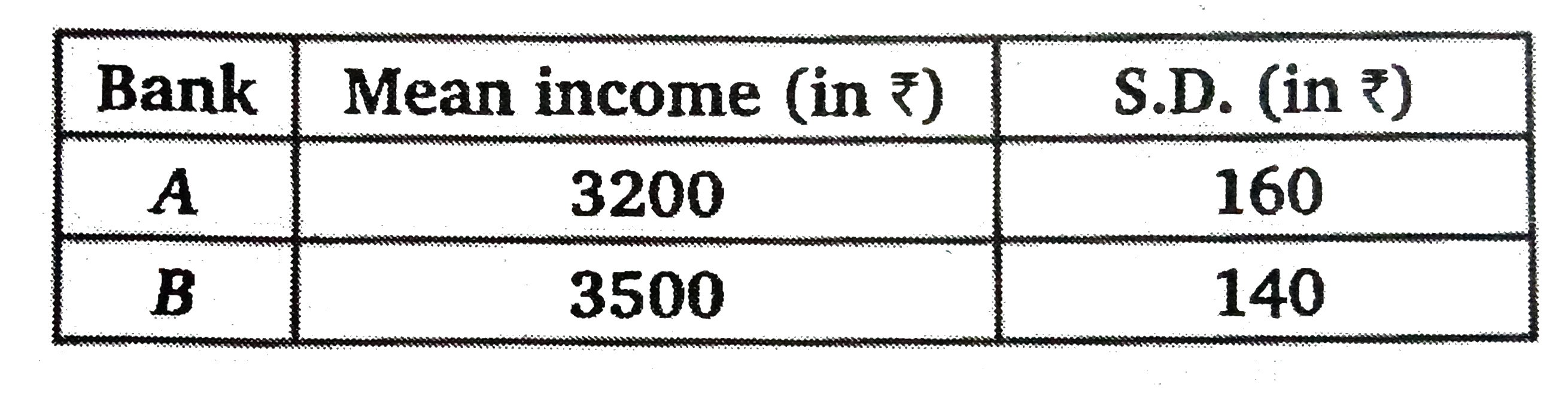If the coefficient of variation of 45% and the mean is 12 then find its s.d ?
The correct Answer is:5.4
To find the standard deviation (s.d.) given the coefficient of variation (CV) and the mean, we can follow these steps:
Step 1: Understand the formula for Coefficient of Variation
The coefficient of variation (CV) is defined as:
CV=Standard Deviation (s.d.)Mean×100
Step 2: Substitute the known values
We know that:
- Coefficient of Variation (CV) = 45%
- Mean = 12
Substituting these values into the formula gives:
45=s.d.12×100
Step 3: Rearrange the formula to solve for Standard Deviation
To isolate the standard deviation, we can rearrange the equation:
s.d.12=45100
Step 4: Multiply both sides by 12
Now, multiply both sides by 12 to solve for s.d.:
s.d.=12×45100
Step 5: Simplify the right side
Calculating the right side:
s.d.=12×0.45=5.4
Conclusion
Thus, the standard deviation is:
s.d.=5.4
The coefficient of variation (CV) is defined as:
We know that:
- Coefficient of Variation (CV) = 45%
- Mean = 12
To isolate the standard deviation, we can rearrange the equation:
Now, multiply both sides by 12 to solve for s.d.:
Calculating the right side:
Thus, the standard deviation is:
Similar Questions
Knowledge Check
The coefficient of variation of distributions are 50 and 60 and their arithmetic means are 30 and 25 respectively. The difference of their standard deviations is
A0B1C1.5D2.5The coefficient of variation of two distributions are 70 and 75 and their standard deviations are 28 and 27 respectively. The difference of their arithmetic means is
A2B3C4D5
If the coefficient of variation of two distribution are 50 ,60 and their arithmetic means are 30 and 25 respectively then the difference of their standard deviation is
View SolutionFind the mean of -12 and 28.
View SolutionIf the coefficients of variations for two distributions are 40 and 50 and their S.D. are 16 and 25 respectively. Find their means.
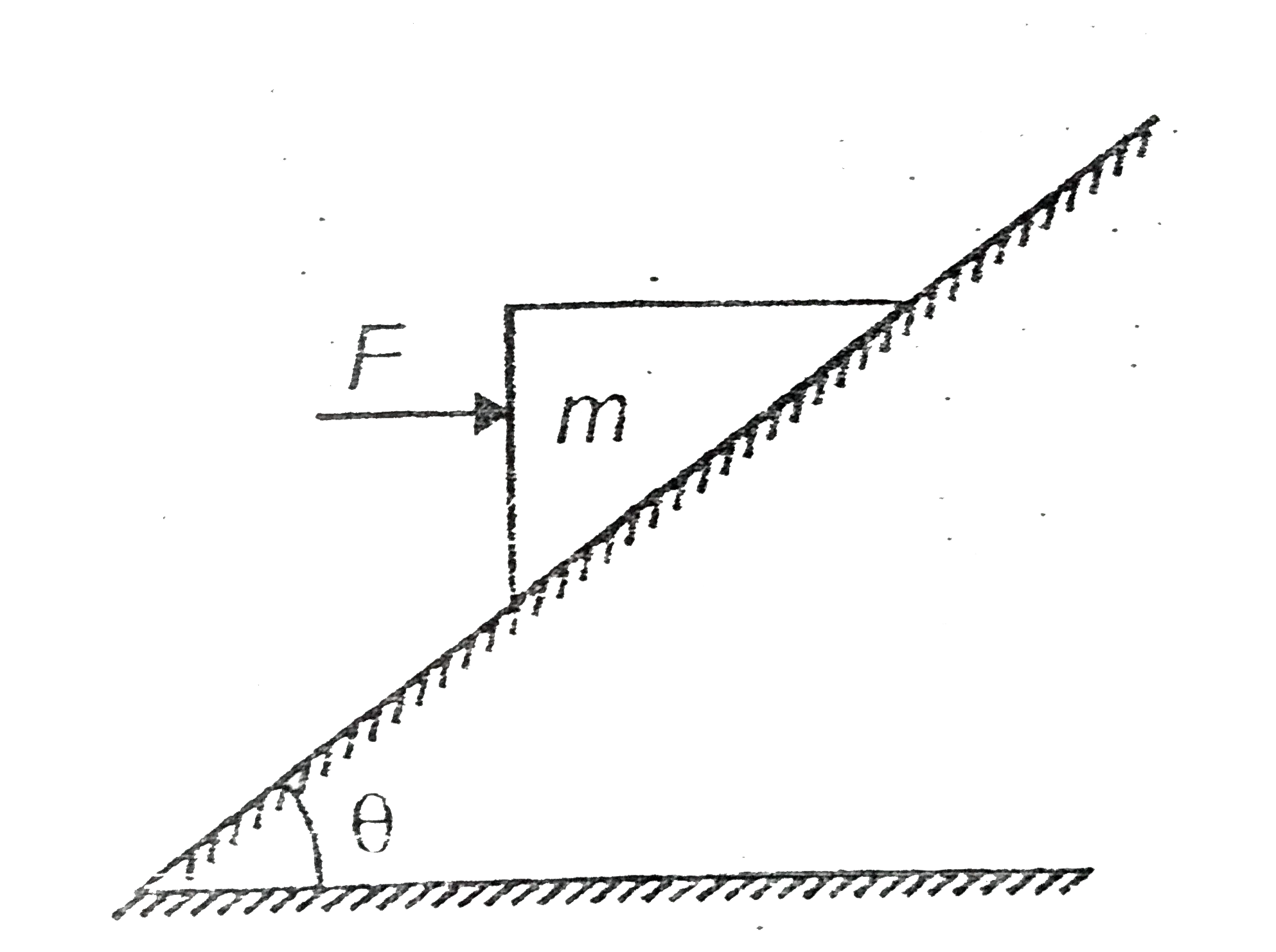
View SolutionA prismatic block of mass m is lifted through a distanced along the slant. If the coefficient of friction between the block and slant surface is 1μ. find the
(A) Work done by force F, friction and gravity.
(B) Speed of the block after moving through a distance d.
Assuming,μ=1/6,θ=45%∘andF=2mg
View SolutionThe coefficient of variation of two distribution are 60 and 70 and their standard deviations are 21 and 16 respectively. Find their arithmeticmeans.
View SolutionIf the mean deviation from the median is 15 and median is 450, then find the coefficient of mean deviation.
View Solution